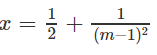Giải và biện luận theo tham số m các phương trình sau Bài 3.17 trang 67 Sách bài tập Đại số 10

Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai

Bài 3.17 trang 67 Sách bài tập Đại số 10: Giải và biện luận theo tham số m các phương trình sau

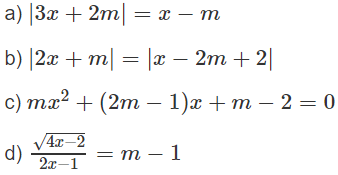
Lời giải:

    a) Với phương trình đã cho trở thành

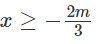
    3x + 2m = x - m ⇔ 2x = -3m ⇔ x = -3m / 2

    Ta có:

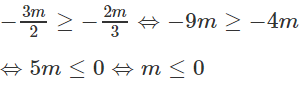
    Với Phương trình đã cho trở thành

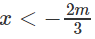
    -3x - 2m = x - m ⇔ 4x = -m ⇔ x = -m / 4

    Ta có:

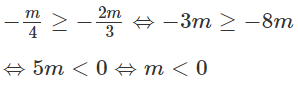
    Kết luận

    Với m > 0 phương trình vô nghiệm;

    Với m = 0 phương trình có nghiệm x = 0;

    Với m < 0 phương trình có nghiệm

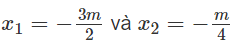
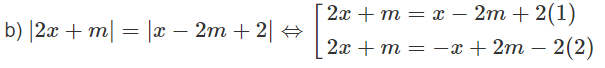
    Phương trình (1) ⇔ x = -3m + 2

    Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3

    Vậy với mọi giá trị của m phương trình có nghiệm là:

    x₁ = -3m + 2 và x₂ = (m - 2) / 3

    c) m = 0 phương trình trở thành

    -x - 2 = 0 ⇒ x = -2

    m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1

    Với m < -1/4 phương trình vô nghiệm;

    Với m ≥ -1/4 nghiệm của phương trình là

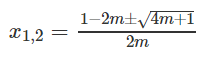
    d) Điều kiện của phương trình là m > 1/2

    Với điều kiện đó vế trái dương, nên vế phải cũng dương nên m > 1. Lúc đó ta có:

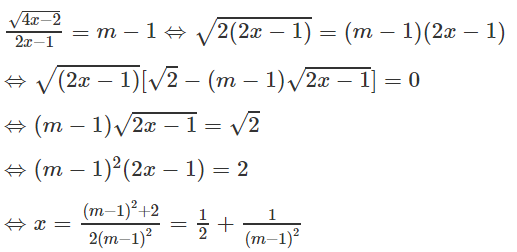
    Giá trị thỏa mãn điều kiện x > 1/2

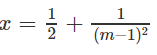
    Kết luận. Với m ≤ 1 phương trình vô nghiệm.

    Với m > 1 nghiệm của phương trình là