Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với sin của góc xen giữa chúng

Bài 3: Các hệ thức lượng trong tam giác và giải tam giác

Bài 2.37 trang 102 Sách bài tập Hình học 10: Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với sin của góc xen giữa chúng.

Lời giải:

    (h.2.29)

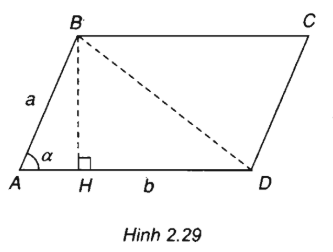
    Xét hình bình hành ABCD có AB = a, AD = b, góc BAD = α và BH là đường cao, ta có BH ⊥ AD tại H

    Gọi S là diện tích hình bình hành ABCD, ta có S = AD. BH với BH = ABsinα

    Vậy S = AD.AB.sinα = a.b.sinα

    Nếu góc BAD = α thì góc ABC = 180^ο - α

    Khi đó ta vẫn có sin BAD = sin ABC

    Nhận xét: Diện tích hình bình hành ABCD gấp đôi diện tích tam giác ABD mà tam giác ABD có diện tích là a.b.sinα/2. Do đó ta suy ra diện tích của hình bình hành bằng a.b.sinα