Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm dương phân biệt

Bài 5: Dấu của tam thức bậc hai

Bài 4.64 trang 123 Sách bài tập Đại số 10: Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm dương phân biệt

    a) x² - 2x + m² + m + 3 = 0;

    b) (m² + m + 3)x² + (4m² + m + 2)x + m = 0

Lời giải:

    Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm dương phân biệt, điều kiện cần và đủ là:

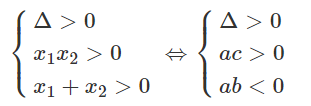
    a) x² - 2x + m² + m + 3 = 0 có Δ' = -m² - m - 2 < 0, ∀m. Do đó không có giá trị nào của m thỏa mãn yêu cầu bài toán.

    b) (m² + m + 3)x² + (4m² + m + 2)x + m = 0 có a = m² + m + 3 > 0, ∀m và có b = 4m² + m + 2 > 0, ∀m, nên ab > 0, ∀m. Vì vậy không có giá trị nào của m để phương trình đã cho có hai nghiệm dương phân biệt.