Cho góc x thỏa mãn điều kiện 0ο < x < 90^ο. Khẳng định nào sau đây là sai

---

Ôn tập chương 2

Bài tập trắc nghiệm trang 106, 107, 108, 109, 110 Sách bài tập Hình học 10:

    Bài 2.68: Cho góc x thỏa mãn điều kiện 0^ο < x < 90^ο. Khẳng định nào sau đây là sai?

    A. sin x > 0                  B. cos x < 0

    C. tan x > 0                  D. cot x > 0

Lời giải:

Khi 0^o < x < 90^o ta có sinx, cosx, tanx, cotx đều dương.

Đáp án: B

    Bài 2.69: Cho góc x thỏa mãn điều kiện 90^ο < x < 180^ο. Khẳng định nào sau đây là đúng?

    A. cos x < 0                  B. sin x < 0

    C. tan x > 0                   D. cot x > 0

Lời giải:

Khi 90^o < x < 180^o, ta có sinx > 0, cosx < 0, tanx < 0, cotx < 0

Đáp án: A

    Bài 2.70: Giá trị của biểu thức m.sin0^ο + n.cos0^ο + p.sin90^ο

    A. n - p                  B. m + p

    C. m - p                  D. n + p

Lời giải:

Ta có sin0^o = 0, cos0^o = 1, sin90^o = 1.

Đáp án: D

    Bài 2.71: Rút gọn biểu thức S = a²sin90^ο + b²cos90^ο + c²cos180^ο, ta có S bằng:

    A. a² + b²                  B. a² - b²

    C. a² - c²                  D. b² + c²

Lời giải:

Ta có sin90^o = 1, cos90^o = 0, cos180^o = -1.

Đáp án: D

    Bài 2.72: Giá trị của biểu thức S = 3 - sin²90^ο + 2cos²60^ο - 3tan²45^ο bằng:

    A. 0,5                  B. -0,5

    C. 1                  D. 3

Lời giải:

sin90^o = 1, cos60^o = 1/2, tan45^o = 1.

Đáp án: B

    Bài 2.73: Cho biểu thức P = 3sin²x + 4cos²x, biết cosx = 0,5, giá trị của P bằng bao nhiêu?

    A. P = 7/4                   B. P = 1/4

    C. P = 7                  D. P = 13/4

Lời giải:

Ta có P = 3(1 - cos² x) + 4cos² x = 3 + cos²x = 3 + 1/4 = 13/4.

Đáp án: A

    Bài 2.74: Trong các khẳng định sau, khẳng định nào sai?

    A. (sinx + cosx)² = 1 + 2sinxcosx

    B. (sinx - cosx)² = 1 - 2sinxcosx

    C. sin⁴x + cos⁴x = 1 - 2.sin²x.cos²x

    D. sin⁶x + cos⁶x = 1 - sin²x.cos²x

Lời giải:

Vì sin⁶x + cos⁶x = 1 - 3sin² x. cos²x

Đáp án: D

    Bài 2.75: Giá trị của biểu thức S = cos²12^ο + cos²78^ο + cos²1^ο + cos²89^ο bằng:

    A. S = 0                   B. S = 1

    C. S = 2                   D. S = 4

Lời giải:

Vì 12^o + 78^o = 90^o nên cos78^o = sin12^o. Tương tự cos89^o = sin1^o.

Ta có S = cos² 12^o + sin² 12^o + cos² 1^o + sin² 1^o.

Đáp án: C

    Bài 2.76: Gọi G là trong tâm tam giác đều ABC có cạnh bằng a. Trong các khẳng định sau, khẳng định nào sai?

Lời giải:

GA = GB = 2/3.(a√3)/2 = (a√3)/3 và (GA→, GB→) = 120^o

Đáp án: C

    Bài 2.77: Cho hình vuông ABCD có cạnh bằng a. Tích vô hướng bằng bao nhiêu?

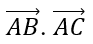
    A. a²                           B. a²/2

    C. 2a²                            D. a²√2

Lời giải:

AB→. AC→ = AB.AC.cos45^o = a.a√2.√2/2 = a².

Đáp án: A

    Bài 2.78: Cho hai vectơ a, b (khác vectơ 0) thỏa mãn: . Trong các khẳng định sau, khẳng định nào đúng:

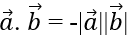
Lời giải:

a→. b→ = -|a→|.|b→| ⇔ |a→|.|b→|. cos(a→, b→) = -|a→|.|b→| ⇔ cos(a→, b→) = -1 nên a→, b→ ngược hướng.

Đáp án: C

    Bài 2.79: Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Tích vô hướng bằng:

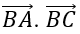
    A. a²                  B. -a²

    C. a²/2                  D. a²√3

Lời giải:

BA→ . BC→ = -AB→(AC→ - AB→) = (-AB→. AC→ ) + AB→² = 0 + a² = a².

Đáp án: A

    Bài 2.80: Trong mặt phẳng Oxy cho tam giác ABC với A(1; 1), B(2; 4), C(10; -2). Giá trị cosC bằng:

Lời giải:

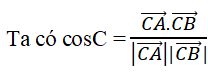
Đáp án: C

    Bài 2.81: Tam giác ABC có AB = 2cm, AC = 1 cm, góc A = 60^ο. Độ dài cạnh là BC là:

    A. 1 cm          B. 2 cm          C. √3 cm          D. √5

Lời giải:

Áp dụng công thức a² = b² + c² – 2bc.cosA ta tính được a = √3 (cm)

Đáp án: C

    Bài 2.82: Tam giác ABC có các cạnh a = 5cm, b = 3cm, c = 5cm. Số đo của góc BAC là:

    A. A = 45^ο                  B. A = 30^ο

    C. A > 60^ο                  D. A = 90^ο

Lời giải:

Áp dụng công thức cosA = (b² + c²-a²)/2bc ta tính được cosA = 3/10 = 0,3.Vậy A ̂ > 60^o.

Đáp án: C

    Bài 2.83: Tam giác ABC có AB = 8cm, BC = 10cm, CA = 6cm. Đường trung tuyến AM của tam giác có độ dài bằng:

    A. 4cm          B. 5cm          C. 6cm          D. 7cm

Lời giải:

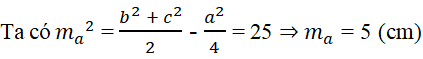
Đáp án: B

    Bài 2.84: Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng:

    A. 1cm          B. √2          C. 2cm          D. 3cm

Lời giải:

Dùng công thức S = pr ta có r = S/p = 2 (cm).

Đáp án: C

    Bài 2.85: Tam giác ABc có các cạnh a = √3cm, b = √2cm, c = 1cm. Đường trung tuyến m_a có độ dài là:

    A. 1cm          B. 1,5cm          C. √3/2cm          D. 2,5cm

Lời giải:

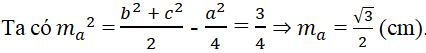
Đáp án: C

    Bài 2.86: Tam giác đều nội tiếp đường tròn bán kính R = 4cm có diện tích là:

    A. 13 cm²                  B. 13√2 cm²

    C. 12√3 cm²                  D. 15 cm²

Lời giải:

Ta có S_ABC = 1/2CH. AB với CH = 3/2R và AB = R√3, mà R = 4 nên S_ABC = 12√3 (cm²).

Đáp án: C

    Bài 2.87: Tam giác ABC vuông và cân tại A có AB = a.

    Đường tròn nội tiếp tam giác ABC có bán kính r bằng:

Lời giải:

Dùng công thức S = pr với .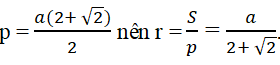

Đáp án: C

    Bài 2.88: Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện:

    (a + b + c)(a + b - c) = 3ab. Khi đó số đo của góc C là:

    A. 120^ο                  B. 30^ο

    C. 45^ο                  D. 60^ο

Lời giải:

(a + b + c)(a + b – c) = 3ab

⇔ (a + b)² - c² = 3ab

⇔ a² + b² + 2ab - c² = 3ab,

Mà a² + b² – 2ab.cosC = c²

Nên 2ab.cosC = ab ⇒ cos C = 1/2 ⇒ ∠C = 60^o.

Đáp án: D

    Bài 2.89: Hình bình hành ABCD có AB = a, BC = a√2 và góc BAD = 45^ο

    Diện tích hình bình hành bằng:

    A. 2a²          B. a²√2          C. a²          D. a²√3

Lời giải:

Cắt hình bình hành theo đường chéo BD rồi ghép cho cạnh BC trùng với AD, ta được một hình vuông cạnh a và S = a².

Đáp án: C

    Bài 2.90: Tam giác ABC vuông cân tại A có AB = AC = a. Đường trung tuyến BM có độ dài là:

    A. 1,5a          B. a√2          C. a√3          D. ( a√5)/2

Lời giải:

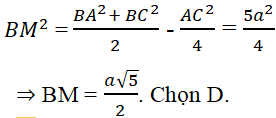
Đáp án: D

    Bài 2.91: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Bán kính R bằng:

Lời giải:

Tam giác đều cạnh a có đường cao h = (a√3)/2.

Mặt khác h = 3/2R (h.2.37)

Do đó: (a√3)/2 = 3/2R ⇔ a√3 = 3R.

Vậy R = (a√3)/3.

Đáp án: C

    Bài 2.92: Bán kính của đường tròn nội tiếp tam giác đều cạnh a bằng:

Lời giải:

Gọi r là bán kính đường tròn nội tiếp tam giác đều cạnh a (h.2.38). Ta có:

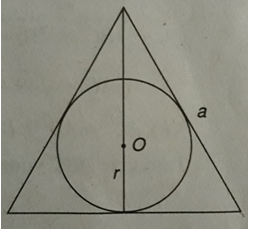
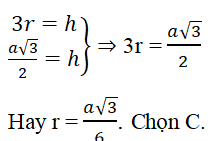
Đáp án: C

    Bài 2.93: Cho tam giác ABC có cạnh BC = a, cạnh CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

    A. 60^ο B. 90^ο C. 150^ο D. 120^ο

Lời giải:

Ta có S = 1/2ab.sinC,

S đạt cực đại khi sinC = 1 nghĩa là ∠C = 90^o.

Đáp án: B

    Bài 2.94: Cho tam giác ABC có diện tích S. Nếu tăng độ dài mỗi cạnh BC và AC lên hai lần đồng thời giữ nguyên độ lớn của góc C thì diện tích của tam giác mới được tạo nên là:

    A. 2S          B. 3S          C. 4S          D. 5S

Lời giải:

Gọi S’ là diện tích của tam giác mới, ta có:

S’ = 1/2.2a.2b.sinC = 2ab.sinC.

Vậy S’ = 4S

Đáp án: C

    Bài 2.95: Cho góc xOy = 30^ο. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 2. Độ dài lớn nhất của đoạn OB bằng:

    A. 2          B. 3          C. 4          D. 5

Lời giải:

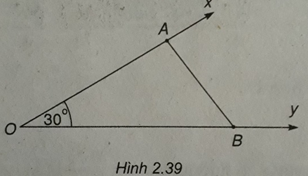
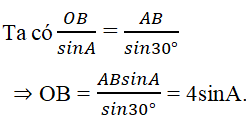
OB đạt cực đại khi sin A = 1 nghĩa là ∠A = 90^o, khi đó OB = 4.

Đáp án: C

    Bài 2.96: Cho hai điểm A(0; 1) và B(3; 0). Khoảng cách giữa hai điểm A và B là:

    A. 3                  B. 4

    C. √5                  D. √10

Lời giải:

Ta có AB→ = (3;1). Do đó |AB→| = √(3²+ 1² ) = √10.

Đáp án: D

    Bài 2.97: Trong mặt phẳng Oxy cho ba điểm A(-1; 1), B(2; 4), C(6; 0). Khẳng định nào sau đây đúng?

    A. Tam giác ABC có ba góc nhọn.

    B. Tam giác ABC có một góc vuông.

    C. Tam giác ABC có một góc tù.

    D. Tam giác ABC đều.

Lời giải:

Ta có AB→ = (3; 3), BC→ = (4; -4)

AB→. BC→ = 0. Vậy tam giác ABC vuông tại B.

Hay ta có |AB→| = √(9+9) = √18

|BC→| = √(16+16)= √32.

AC→ = √(49+1)= √50.

Vậy AC²= AB² + BC².

Tam giác ABC vuông tại B có cạnh huyền là AC.

Đáp án: B