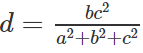Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy

Bài 3: Khái niệm về thể tích của khối đa diện

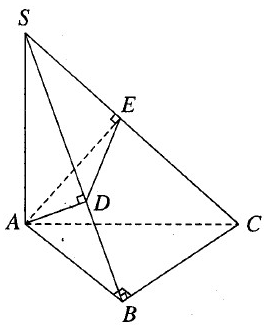
Bài 1.12 trang 18 Sách bài tập Hình học 12: Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c.

a) Hãy tính thể tích khối chóp S.ADE

b) Tính khoảng cách từ E đến mặt phẳng (SAB).

Lời giải:

a) Ta có

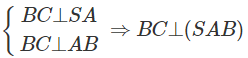
Vì AD ⊂ (SAB) nên AD ⊥ BC

Mặt khác AD ⊥ SB nên AD ⊥ (SBC)

Từ đó suy ra AD ⊥ SC

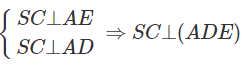
⇒ SC ⊥ DE hay SE ⊥ (ADE)

Trong tam giác vuông SAB ta có: SA.AB = AD.SB

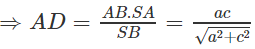
Tương tự, trong tam giác vuông SAC ta có:

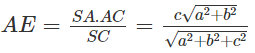
Do AD ⊥ (SBC) nên AD ⊥ DE. Từ đó suy ra:

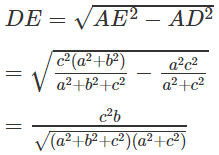
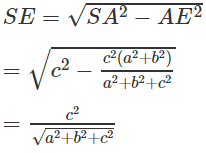
Vậy

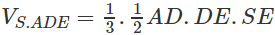
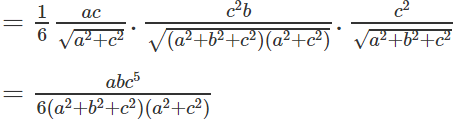
b) Gọi d là khoảng cách từ E đến mặt phẳng (SAB)

Ta có:

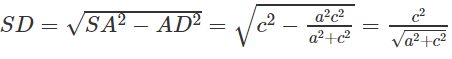
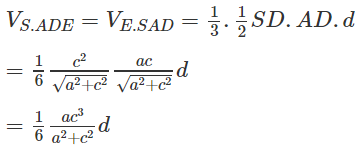
Kết hợp với kết quả trong câu a)

ta suy ra