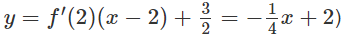Tính diện tích của hình phẳng giới hạn bởi các đường sau y = |x2 – 1| và y = 5 + |x|

Ôn tập cuối năm

Bài 19 trang 219 Sách bài tập Giải tích 12: Tính diện tích của hình phẳng giới hạn bởi các đường sau:

a) y = |x2 – 1| và y = 5 + |x|

b) 2y = x² + x – 6 và 2y = -x² + 3x + 6

c) ,x=1 và tiếp tuyến với đường tại điểm (2; 3/2)

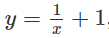
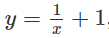
Lời giải:

a) Hai hàm số y = |x2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở Hình 8. Do tính đối xứng qua trục tung, ta có:

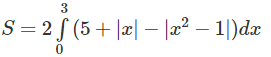
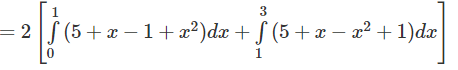
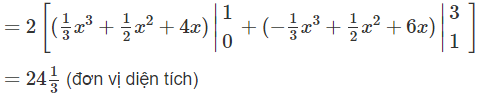
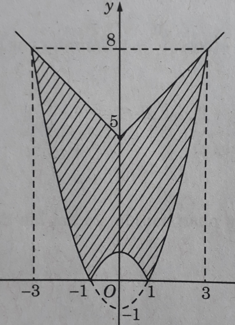
b) Miền cần tính diện tích được thể hiện bởi Hình 9 (học sinh tự làm)

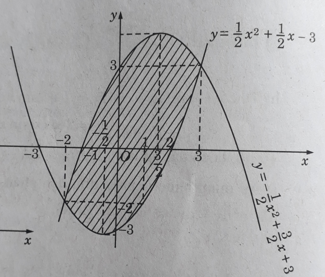
Như vậy, với mọi x ∈ (-2;3) đồ thị của hàm số

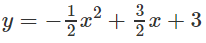
nằm phía trên đồ thị của hàm số

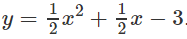
Vậy ta có:

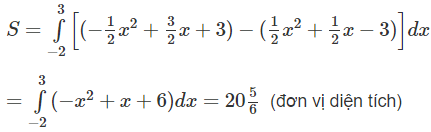
c) Miền cần tính diện tích được thể hiện trên Hình 10:

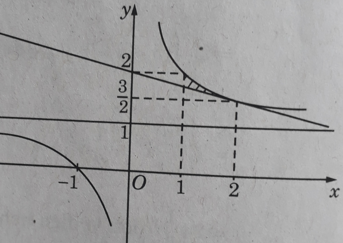
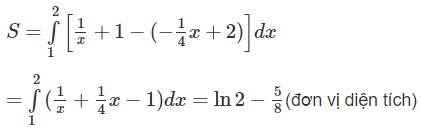
(vì tiếp tuyến với đồ thị của

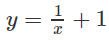
tại điểm (2;3/2) có phương trình là