Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB và AD

Đề toán tổng hợp ôn tập cuối năm

Bài 2 trang 168 Sách bài tập Hình học 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB và AD, H là giao điểm của MD và NC. Biết rằng SH là đường cao của hình chóp đã cho và cạnh SC tạo với đáy hình chóp đó một góc bằng 60^o

a) Thể tích hình chóp S.CDNM

b) Tính khoảng cách giữa DM và SC.

Lời giải:

a) Xét các hình vuông ABCD. Ta có hai tam giác vuông ADM và DCN bằng nhau nên ∠DMA = ∠CND. Từ đó suy ra DM ⊥ CN. Trong tam giác vuông CDN ta có:

CD² = CH.CN ⇒ CH = 2a/√5

Suy ra SH = CH.tan60^o =

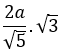
S_CDNM = S_ABCD - S_AMN - S_BCM = 5a²/8

V_S.CDNM =

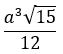
b) Gọi I là chân đường vuông góc kẻ từ H lên SC

Vì MD ⊥ (SCN), MD ∩ (SCN) = H nên

d(MD, SC) = d(H, SC) = HI = HC.sin60^o =