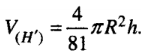Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h

Đề toán tổng hợp ôn tập cuối năm

Bài 4 trang 169 Sách bài tập Hình học 12:Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h.

Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H).

a) Tính tỉ số thể tích của (H') và (H);

b) Xác định r để (H') có thể tích lớn nhất.

Lời giải:

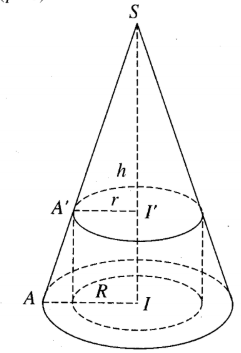
a) Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.

Khi đó

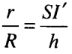
Do đó

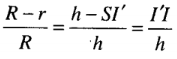
Từ đó suy ra

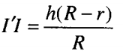
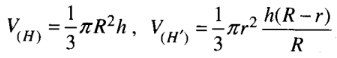
Do đó

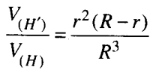
b) V_(H') lớn nhất khi f(r) = r²(R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3r² = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.

Khi đó