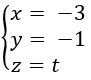Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: x/-3 = y/-1 = x/2

---

Đề toán tổng hợp ôn tập cuối năm

Bài 5 trang 169 Sách bài tập Hình học 12: Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d:

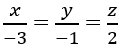
a) Viết phương trình mặt phẳng (P) đi qua A, song song với d, sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P).

b) Tìm tập hợp những điểm cách đều ba điểm A, B, C.

Lời giải:

a) Có hai trường hợp xảy ra:

Trường hợp 1:

(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là v→(-3; -1; 2) và BC→(-2; 4; 0).

Do đó n_P→ = v→ ∧ BC→ = (-8; -4; -14).

Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0

Trường hợp 2:

(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.

Ta có: FA→(0; 1; 0), FA→ ∧ v→ = (2; 0; 3).

Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.

b) Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.

Những điểm cách đều ba điểm A, B, C là giao tuyến Δ = (Q) ∩ (R).

(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n_Q→ = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0

(R) đi qua trung điểm F(1; 1; 1) của BC và có n_R→ = BC→ = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0

Ta có: n_Q→ ∧ n_R→ = (0; 0; -2).

Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)

Suy ra Δ là đường thẳng đi qua D và có vectơ chỉ phương u→(0; 0; 1)

nên có phương trình là: