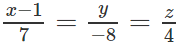Viết phương trình của đường thẳng Δ nằm trong mặt phẳng (α): x + 2z = 0 và cắt hai đường kính

Bài 3: Phương trình đường thẳng

Bài 3.32 trang 130 Sách bài tập Hình học 12: Viết phương trình của đường thẳng Δ nằm trong mặt phẳng (α): x + 2z = 0 và cắt hai đường kính

và

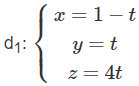
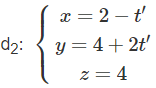
Lời giải:

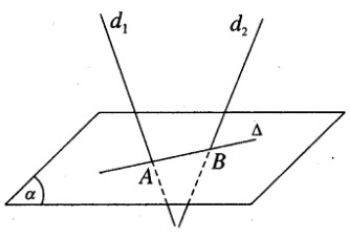
Gọi A và B lần lượt là giao điểm của d₁ và d₂ với (α). Đường thẳng Δ cần tìm chính là đường thẳng AB.

Ta có: A(1 − t; t; 4t) ∈ d₁

A ∈ (α) ⇔ t + 4.(2t) = 0 ⇔ t = 0

Suy ra: A(1; 0; 0)

Ta có : B(2 − t′; 4 + 2t′; 4) ∈ d2

B ∈ (α) ⇔ 4 +2t′ + 8 = 0 ⇔ t′ = −6

Suy ra B(8; -8; 4)

Δ đi qua A, B nên có vecto chỉ phương a_Δ→− = AB→ = (7; −8; 4)

Phương trình chính tắc của Δ là: