Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau

Bài 3: Phương trình đường thẳng

Bài 3.35 trang 130 Sách bài tập Hình học 12: Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau

a) và (α): x + 2y + z - 3 = 0

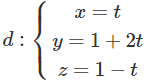
b) và (α): x + z + 5 = 0

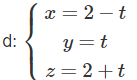
c) và (α): x + y + z -6 = 0

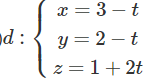
Lời giải:

a) Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng (α) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0

⇔ 4t = 0 ⇔ t = 0

Vậy đường thẳng d cắt mặt phẳng (α) tại M₀(0; 1; 1).

b) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của (α) ta được: (2 – t) +(2 + t) + 5 = 0 ⇔ 0t = -9

Phương trình vô nghiệm, vậy đường thẳng d song song với (α)

c) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của (α) ta được: (3 – t) + (2 – t) + (1 + 2t) – 6 = 0 ⇔ 0t = 0

Phương trình luôn thỏa mãn với mọi t. Vậy d chứa trong (α) .