Cho hai bộ ba điểm: A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1); M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1)

Bài 1: Hệ tọa độ trong không gian

Bài 3.4 trang 103 Sách bài tập Hình học 12: Cho hai bộ ba điểm:

a) A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1)

b) M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1)

Hỏi bộ nào có ba điểm thẳng hàng?

Lời giải:

a) Ta có: AB→ = (−1; −2; 1)

Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB→ và AC→ cùng phương, nghĩa là AB→ = kAC→ với k là một số thực.

Giả sử ta có AB→ = kAC→

khi đó

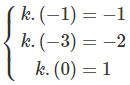
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.

b) Ta có: MN→ = (−5; 2; 0) và MP→ = (−10; 4; 0). Hai vecto MN→ và MP→ thỏa mãn điều kiện: MN→ = kMP→ với k = k/2 nên ba điểm M, N, P thẳng hàng.