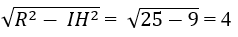Trong không gian Oxyz, cho mặt cầu (S): x^2 + y^2 + z^2 - 2x + 4y + 2z - 19 = 0

Đề toán tổng hợp ôn tập cuối năm

Bài 8 trang 169 Sách bài tập Hình học 12: Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² - 2x + 4y + 2z - 19 = 0

và mặt phẳng (P): x - 2y + 2z - 12 = 0

a) Chứng minh rằng (P) cắt (S) theo một đường tròn.

b) Tìm tọa độ tâm và bán kính của đường tròn đó.

Lời giải:

a) Mặt cầu (S) tâm I(1; -2; -1) bán kính R = 5

d(I,(P)) = 3 < R

Do đó (P) cắt (S) theo một đường tròn, gọi đường tròn đó là (C).

b) Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là

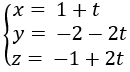
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).

Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0

Suy ra t = 1, do đó H = (2; -4; 1).

Bán kính của (C) bằng