Hãy tìm tọa độ các đỉnh còn lại. Chứng minh A'C ⊥ (BC'D). Tìm tọa độ của chân đường vuông góc chung

Đề toán tổng hợp ôn tập cuối năm

Bài 9 trang 170 Sách bài tập Hình học 12:

a) Hãy tìm tọa độ các đỉnh còn lại.

b) Chứng minh A'C ⊥ (BC'D)

c) Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.

Lời giải:

a) Dễ thấy C(1; 1; 0), B'(1; 0; 1), D'(0; 1; 1), C'(1; 1; 1), D'(0; 1; 1).

b) Ta có: A'C→ = (1; 1; -1)

BC'→ = (0; 1; 1)

BD→ = B'D'→ = (-1; 1; 0)

do đó A'C→.BC'→ = 0 và A'C→.BD→ = 0

Từ đó suy ra A'C ⊥ (BC'D).

c)

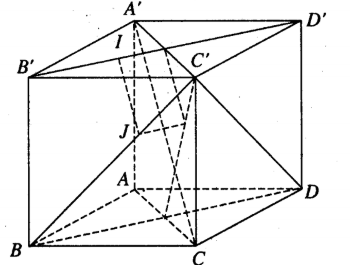
Gọi IJ là đường vuông góc chung của B'D' và BC', n₁→ là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với AC', n₂→ là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.

Khi đó n₁→ = A'C→ ∧ B'D'→ = (1; 1; 2)

n₂→ = A'C→ ∧ BC'→ = (2; -1; 1)

Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.

Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.

Phương trình của (B'D') là: x = 1 - t, y = t, z = 1.

Phương trình của (BC') là: x = 1, y = t, z = t.

I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)

Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = 1/3. Từ đó suy ra I(2/3; 1/3; 1)

Tương tự, ta tìm được J(1; 2/3; 1/3).