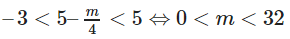Cho hàm số. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho. Tìm các giá trị của tham số m

Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Giải bài 60 trang 36 SBT Giải tích 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.60 trang 36 Sách bài tập Giải tích 12: Cho hàm số:

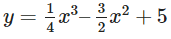
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho

b) Tìm các giá trị của tham số m để phương trình x³ – 6x² + m = 0 có 3 nghiệm thực phân biệt.

Lời giải:

a) Tập xác định: D = R;

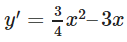
y′= 0 ⇔

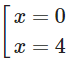
Hàm số đồng biến trên mỗi khoảng (–∞; 0), (4; +∞).

Hàm số nghịch biến trên mỗi khoảng (0; 4).

Hàm số đạt cực đại tại x = 0, y_CĐ = 5. Hàm số đạt cực tiểu tại x = 4, y_CT = -3.

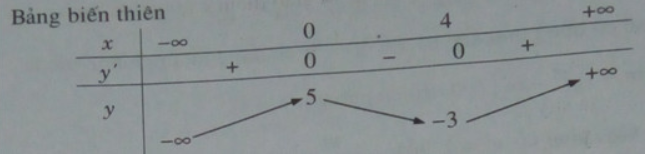
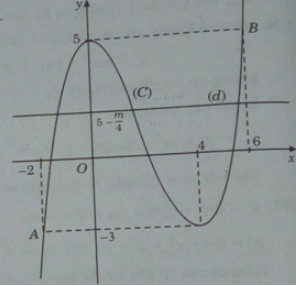
Đồ thị đi qua A(-2; -3); B(6;5).

b) x³ – 6x² + m = 0

⇔ x³ – 6x² = –m (1)

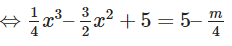
Số nghiệm thực phân biệt của phương trình (1) bằng số giao điểm phân biệt của đồ thị (C)

và đường thẳng

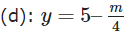
Suy ra (1) có 3 nghiệm thực phân biệt khi và chỉ khi: