Biện luận theo k số nghiệm của phương trình: (x − 1)^2 = 2|x − k|; (x + 1)^2 . (2 − x) = k
Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải bài 62 trang 37 SBT Giải tích 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.
Bài 1.62 trang 37 Sách bài tập Giải tích 12: Biện luận theo k số nghiệm của phương trình:
a) (x − 1)2 = 2|x − k|
b) (x + 1)2.(2 − x) = k
Lời giải:
a) Phương trình đã cho tương đương với phương trình:
2(x − k) = (x − 1)2 hoặc 2(x − k) = -(x − 1)2
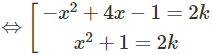
Ta vẽ đồ thị của hai hàm số: y = −x2 + 4x – 1 và y = x2 + 1
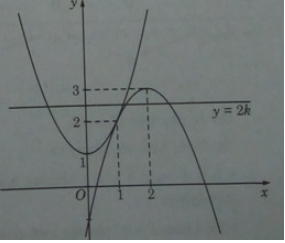
Từ đồ thị ta suy ra:
• 2k > 3 : phương trình có hai nghiệm;
• 2k = 3 : phương trình có ba nghiệm;
• 2 < 2k < 3 : phương trình có bốn nghiệm;
• 2k = 2 : phương trình có ba nghiệm;
• 1 < 2k < 2 : phương trình có bốn nghiệm ;
• 2k = 1 : phương trình có ba nghiệm ;
• 2k < 1 : phương trình có hai nghiệm.
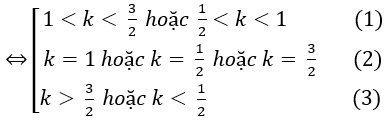
(1) : phương trình có bốn nghiệm;
(2): phương trình có ba nghiệm ;
(3): phương trình có hai nghiệm.
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = (x + 1)2.(2 − x).
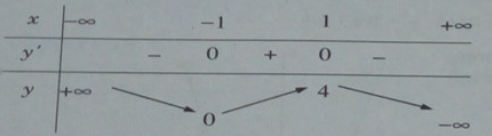
y = −x3 + 3x + 2 ⇒ y′ = −3x2 + 3
y′=0 ⇔
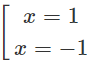
Bảng biến thiên:
Đồ thị:
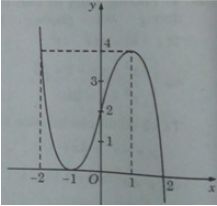
Từ đồ thị hàm số ta suy ra:
• k > 4 hoặc k < 0: phương trình có một nghiệm;
• k = 4 hoặc k = 0 : phương trình có hai nghiệm;
• 0 < k < 4: phương trình có ba nghiệm.

