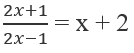Bài tập trắc nghiệm trang 38, 39 Sách bài tập Giải tích 12

---

Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Giải bài tập trắc nghiệm trang 38, 39 SBT Giải tích 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài tập trắc nghiệm trang 38, 39 Sách bài tập Giải tích 12:

Bài 1.68: Hàm số y = x³ + (m + 3)x² + mx - 2 đạt cực tiểu tại x = 1 khi:

A. m = 1              B. m = 2

C. m = -3              D. m = 4

Bài 1.69: Hàm số y = x⁴ + (m² - 4)x² + 5 có ba cực trị khi:

A. -2 < m < 2              B. m = 2

C. m < -2              D. m > 2

Bài 1.70: Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:

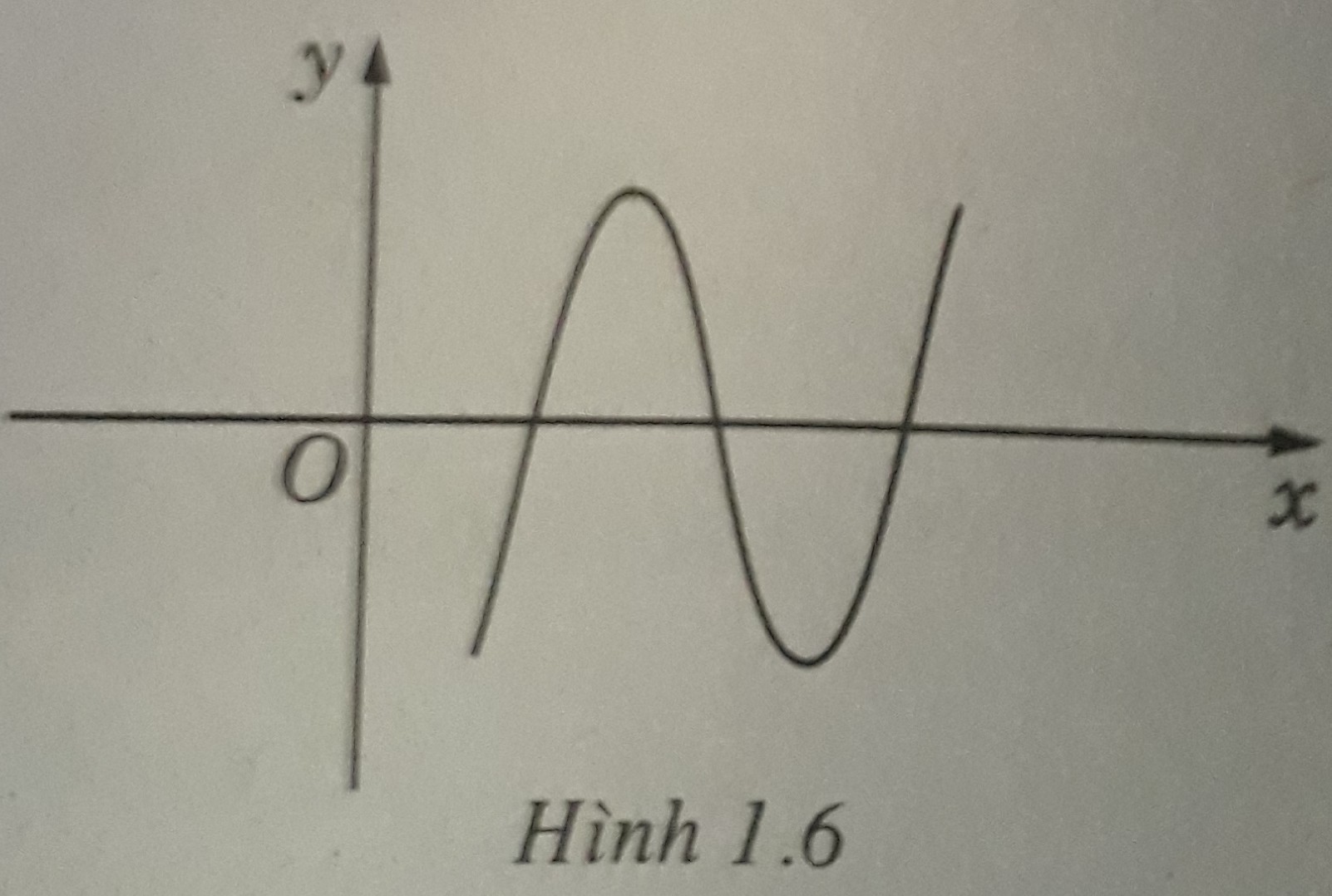
A. y = ax² + bx + c với a ≠ 0

B. y = ax³ + cx + d với a < 0

C. y = ax³ + bx² + cx + d với a > 0 và b² - 3ac > 0

D. y = x³

Bài 1.71: Xác định giá trị của tham số m để hàm số

y = x³ - 3(m - 1)x² - 3(m + 1)x - 5 có cực trị

A. m > 0              B. -1 < m < 1

C. m ≤ 0              D. ∀m ∈ R.

Bài 1.72: Phương trình tiếp tuyến của đồ thị hàm số y = x⁴ - 2x² tại điểm có hoành độ x = -2 là:

A. y = -24x + 40              B. y = 24x - 40

C. y = -24x - 40              D. y = -24x

Bài 1.73: Phương trình tiếp tuyến của đồ thị hàm số y = x⁴ - 2x² - 3 song song với đường thẳng y = 24x - 1 là:

A. y = 24x - 43              B. y = -24x - 43

C. y = 24x + 43              D. y = 24x + 1

Bài 1.74: Giao điểm của đồ thị hàm số và đường thẳng y = x + 2 là:

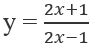
A. (1;3) và (-3/2; 1/2)              B. (1;3) và (0;2)

C. (0; -1) và (-3/2; 1/2)              D. (0; -1) và (0;2)

Lời giải:

Đáp án và hướng dẫn giải

Bài	1.68	1.69	1.70	1.71	1.72	1.73	1.74
Đáp án	C	A	C	D	C	A	A

Bài 1.68: Đáp án: C.

y' = 3x² + 2(m + 3)x + m

y'(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = -3

Với m = -3, y' = 3x² - 3 ⇒ y''(x) = 6x.

Vì y''(1) = 6 > 0 nên hàm số đạt cực tiểu khi m = -3.

Bài 1.69: Đáp án: A.

Hàm số y = x⁴ + (m² - 4)x² + 5 có 3 cực trị khi y' = 0 có 3 nghiệm phân biệt, tức là

y' = 4x³ + 2(m² - 4) = 2x(2x² + m² - 4) = 0 có ba nghiệm phân biệt

⇔ 2x² + m² - 4 = 0 có hai nghiệm phân biệt khác 0.

⇔ 4 - m² > 0 ⇔ -2 < m < 2.

Bài 1.70: Đáp án: C.

Bài 1.71: Đáp án: D.

y' = 3x² - 6(m - 1)x - 3(m + 1)

y' = 0 ⇔ x² - 2(m - 1)x - m - 1 = 0

Δ' = (m - 1)² + m + 1 = m² - m + 2 ≥ 0

Tam thức m² - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.

Bài 1.72: Đáp án: C.

y' = 4x³ - 4x = 4x(x² - 1). Ta có

y - y(-2) = y'(-2)(x + 2) ⇔ y - 8 = -24(x + 2) ⇔ y = -24x - 40.

Bài 1.73: Đáp án: A.

y' = 4x³ - 4x.

Tiếp tuyến phải tìm đi qua điểm có hoành độ thỏa mãn

4x³ - 4x = 24 ⇔ x³ - x - 6 = 0 ⇔ (x - 2)(x² + 2x + 3) = 0 ⇔ x = 2.

Do đó phương trình tiếp tuyến phải tìm là

y - y(2) = 24(x - 2) ⇔ y = 24x - 43.

Bài 1.74: Đáp án: A.

Gợi ý: Thử trực tiếp vào phương trình