Cho hàm số y = 2x^4 − 4x^2 (1). Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1)

Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Giải bài 64 trang 37 SBT Giải tích 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.64 trang 37 Sách bài tập Giải tích 12: Cho hàm số y = 2x⁴ − 4x² (1)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).

b) Với giá trị nào của m, phương trình x²|x² − 2| = m có đúng 6 nghiệm thực phân biệt?

(Đề thi đại học năm 2009; khối B)

Lời giải:

a) Tập xác định: D = R

y′=0 ⇔

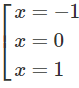
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; +∞)

Hàm số nghịch biến trên mỗi khoảng (−∞; −1); (0; 1)

Hàm số đạt cực đại tại x = 0; y_CĐ = 0

Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y_CT = −2

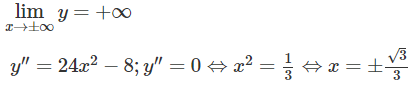
Đồ thị có hai điểm uốn:

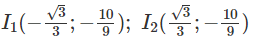
Bảng biến thiên:

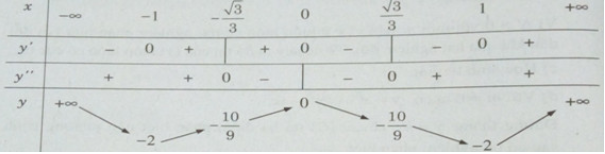
Đồ thị:

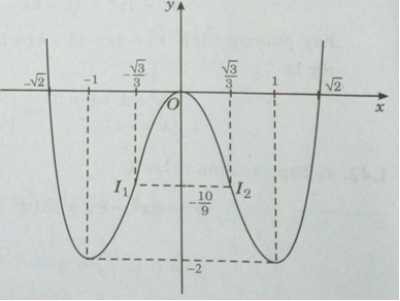
Đồ thị cắt trục hoành tại:

b) Ta có: x²|x² − 2| = m

⇔ 2x² |x² − 2| = 2m

⇔|2x²(x² − 2)| = 2m

⇔|2x⁴ − 4x²| = 2m

Từ đồ thị hàm số y = 2x⁴ – 4x² có thể suy ra đồ thị của hàm số y = |2x⁴ − 4x²| như sau:

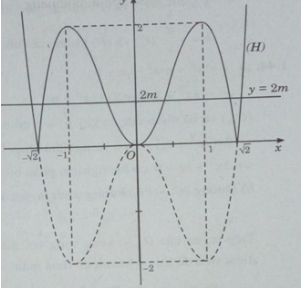
Phương trình: |2x⁴ − 4x²| = 2m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m có 6 nghiệm phân biệt với đồ thị (H)

⇔ 0 < 2m < 2

⇔ 0 < m < 1