Cho hàm số: y= (4 - x) / (2x + 3m). Xét tính đơn điệu của hàm số. Chứng minh rằng với mọi m

Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Giải bài 67 trang 38 SBT Giải tích 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.67 trang 38 Sách bài tập Giải tích 12: Cho hàm số:

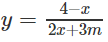
a) Xét tính đơn điệu của hàm số.

b) Chứng minh rằng với mọi m, tiệm cận ngang của đồ thị (C_m) của hàm số đã cho luôn đi qua điểm

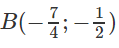
c) Biện luận theo m số giao điểm của (C_m) và đường phân giác của góc phần tư thứ nhất.

d) Vẽ đồ thị của hàm số:

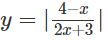
Lời giải:

Xét hàm số:

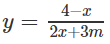
a) TXĐ: R \ {−3m/2}

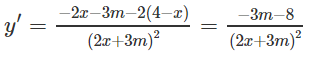
    +) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng

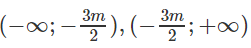
    +) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng

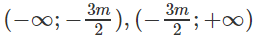
    +) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4

b) Ta có:

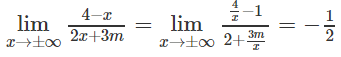
nên với mọi m, đường thẳng y = -1/2 là tiệm cận ngang và đi qua

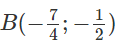
c) Số giao điểm của (C_m) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:

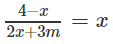
Ta có:

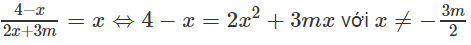
⇔ 2x² + (3m + 1)x – 4 = 0 ⇔ 2x² + (3m + 1) x – 4 = 0 với x ≠ −3m/2

    +) Thay x = −3m/2 vào (*), ta có:

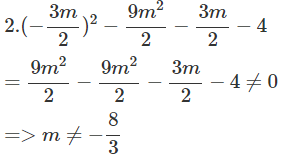
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m ≠ −8/3.

Ta có: Δ = (3m + 1)² + 32 > 0, ∀ m. Từ đó suy ra với m ≠−8/3 đường thẳng y = x luôn cắt (C_m) tại hai điểm phân biệt.

d) Ta có:

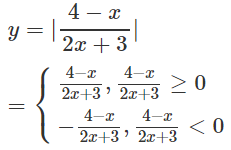
Trước hết, ta vẽ đồ thị (C) của hàm số

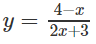
TXĐ: D = R \ {−3/2}.

Vì

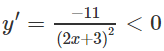
với mọi nên hàm số nghịch biến trên các khoảng

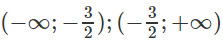
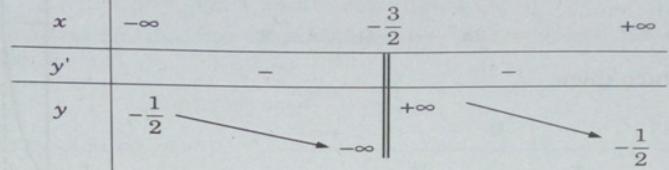
Bảng biến thiên:

Tiệm cận đứng x = −3/2

Tiệm cận ngang y = −1/2

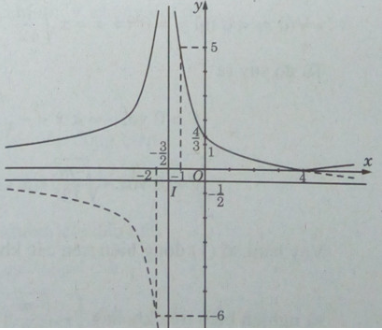
Đồ thị (C) đi qua các điểm (−2;−6),(−1;5),(0;4/3),(4;0)

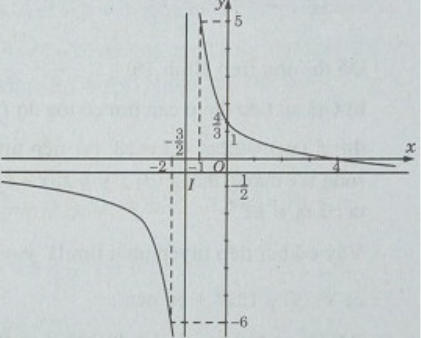
Để vẽ đồ thị (C’) của hàm số , ta giữ nguyên phần đồ thị (C) nằm phía trên trục hoành và lấy đối xứng phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.