Bài 11.3, 11.4, 11.5, 11.6, 11.7 trang 30 SBT Toán 7 tập 1
Bài 11.3, 11.4, 11.5, 11.6, 11.7 trang 30 SBT Toán 7 tập 1
Bài 11.3: Không dùng bảng số hoặc máy tính, hãy so sánh:
√(40+2) với √40 + √2.
Lời giải:
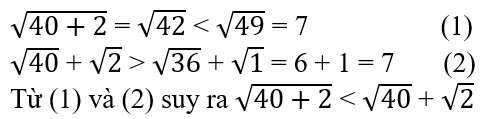
Bài 11.4:
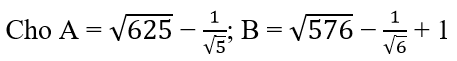
Hãy so sánh A và B.
Lời giải:
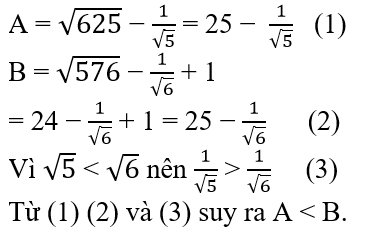
Bài 11.5:
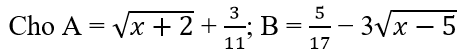
a) Tìm giá trị nhỏ nhất của A.
b) Tìm giá trị lớn nhất của B.
Lời giải:
a) Ta có:
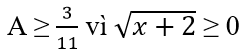
A đạt giá trị nhỏ nhất là 3/11 khi và chỉ khi x = -2.
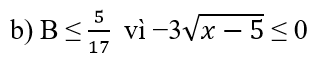
Vậy B đạt giá trị lớn nhất là 5/17 khi và chỉ khi x = 5.
Bài 11.6:
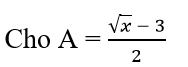
Tìm x ∈ Z và x < 30 để A có giá trị nguyên.
Lời giải:
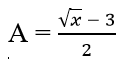
có giá trị nguyên nên (√x - 3) ⋮ 2.
Suy ra x là số chính phương lẻ.
Vì x < 30 nên x ∈ {12; 32; 52} hay x ∈ {1; 9; 25}.
Bài 11.7:
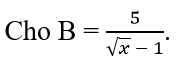
Tìm x ∈ Z để B có giá trị nguyên.
Lời giải:
Khi x là số nguyên thì √x hoặc là số nguyên (nếu x là số chính phương) hoặc là số vô tỉ (nếu x không phải số chính phương).
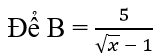
là số nguyên thì √x không thể là số vô tỉ, do đó √x là số nguyên và √x - 1 phải là ước của 5 tức là √x - 1 ∈ Ư(5). Để B có nghĩa ta phải có x ≥ 0 và x ≠ 1. Ta có bảng sau:
| √x - 1 | 1 | -1 | 5 | -5 |
| √x | 2 | 0 | 6 | -4(loại) |
| x | 4 | 0 | 36 | |
Vậy x ∈ {4; 0; 36} (các giá trị này đều thoả mãn điều kiện x ≥ 0 và x ≠ 1).

