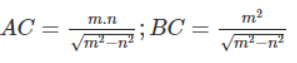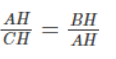Bài 8.1, 8.2, 8.3 trang 96 SBT Toán 8 tập 2

---

Bài 8.1, 8.2, 8.3 trang 96 SBT Toán 8 tập 2

Bài 8.1 trang 96 sách bài tập Toán 8 Tập 2: Cho góc nhọn xOy.

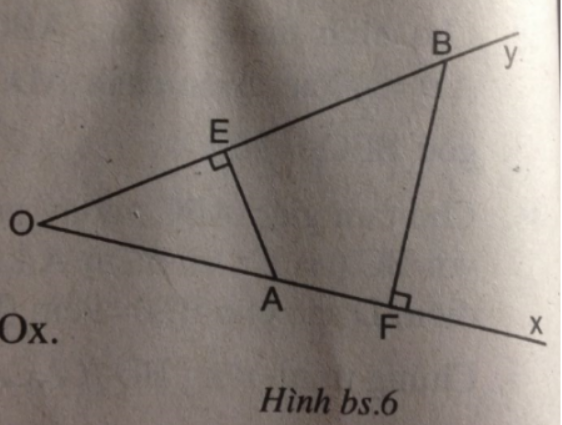
Trên tia Ox lấy một điểm A sao cho OA = 8,65cm.

Trên tia Oy lấy một điểm B sao cho OB = 15,45cm

Vẽ AE vuông góc với Oy, BF vuông góc với Ox.

Biết độ dài đoạn thẳng BF = 10,25cm.

Độ dài đoạn thẳng AE (lấy chính xác đến hai chữ số thập phân) là:

A. 13,04 cm

B. 18,31 cm

C. 5,74 cm

D. 5,73 cm

Lời giải:

Chọn C

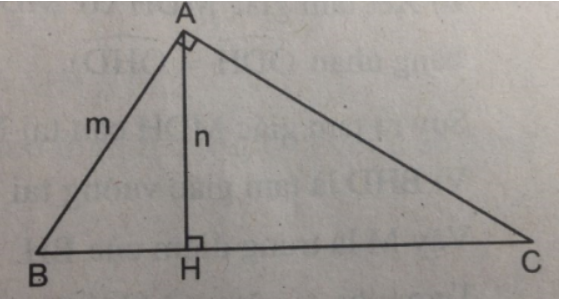
Bài 8.2 trang 96 sách bài tập Toán 8 Tập 2: Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm. Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)

Lời giải:

Xét hai tam giác ABC và HBA, ta có: ∠BAC = ∠BHA = 1v

Góc B là góc nhọn chung

Vậy ΔABC đồng dạng ΔHBA

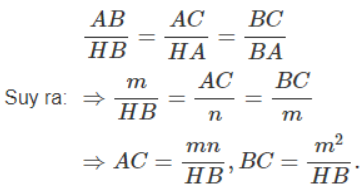
Xét tam giác vuông ABH, ta có:

HB = √(AB²−AH²) = √(m²−n²)

Từ đó, ta có:

Với m = 12,5cm, n = 10,85cm, ta tính được:

AC ≈ 21,85cm; BC ≈ 25,17cm.

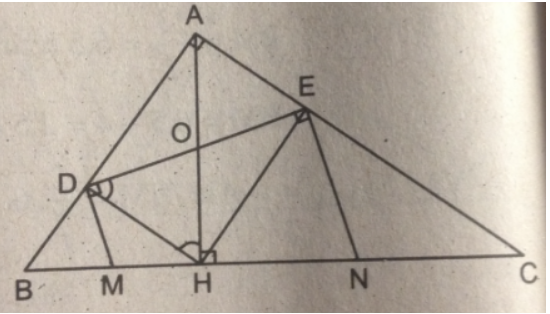
Bài 8.3 trang 96 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.

Gọi D và E là hình chiếu của H trên AB và AC.

a. Tính độ dài DE

b. Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.

c. Tính diện tích tứ giác DENM.

Lời giải:

a. Xét hai tam giác vuông ABH và CAH có:

∠ABH = ∠CAH (cùng phụ với góc ∠BAH)

Do đó ∆ ABH đồng dạng ∆ CAH (g.g).

Suy ra:

⇒AH² = BH.CH = 4.9 ⇒ AH = 4.9 = 6(cm)

Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.

Suy ra: DE = AH = 6 (cm)

b. Xét tam giác MDH có ∠MDH = ∠MHD (vì cùng bằng góc vuông trừ đi góc bằng nhau ∠ODH = ∠OHD )

Suy ra tam giác MDH cân tại M, do đó MD = MH. (1)

Vì BHD là tam giác vuông tại D nên MD = BM.

Vậy M là trung điểm của BH

Tương tự, ta cũng có N là trung điểm của CH.

c. Theo chứng minh trên, ta có:

DM = MH = 1/2 BH = 1/2.4 = 2(cm)

EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)

DE = AH = 6(cm)

DENM là hình thang vuông, do đó diện tích của nó là:

S_DENM = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5(cm²).