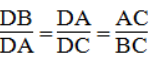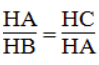Bài 49, 50 trang 96 SBT Toán 8 tập 2

---

Bài 49, 50 trang 96 SBT Toán 8 tập 2

Bài 49 trang 96 sách bài tập Toán 8 Tập 2: Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm; Tính độ dài các cạnh của tam giác vuông.

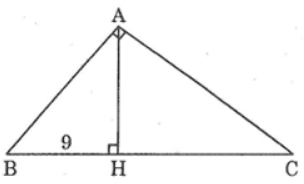
Lời giải:

Xét hai tam giác vuông DAC và DBA ,ta có:

∠(ADC) = ∠(BDA) = 90^o

∠C = ∠(DAB) (hai góc cùng phụ ∠B )

Suy ra: ΔDAC đồng dạng ΔDBA (g.g)

Suy ra:

⇒ DA² =DB.DC

hay DA = √(DB.DC) = √(9.16) = 12 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:

AB² = DA² + DB² = 9² + 12² = 225 => AB =15 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:

AC² = DA² + DC² = 12² +16² = 400 ⇒ AC = 20cm

Vậy BC = BD + DC = 9 + 16 = 25(cm)

Bài 50 trang 96 sách bài tập Toán 8 Tập 2: Tam giác vuông ABC (A = 90^o) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm

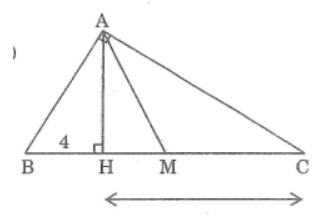
Lời giải:

Xét hai tam giác vuông HBA,HAC có:

∠(BHA) = ∠(AHC) = 90^o

∠B = ∠(HAC) (hai góc cùng phụ ∠C )

⇒ ΔHBA đồng dạng ΔHAC (g.g)

Suy ra:

⇒ HA² = HB.HC = 4.9 = 36(cm)

Suy ra: AH = 6(cm)

Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6.5cm

Mà HM = BM – BH = 6,5 – 4 = 2,5cm

Vậy S_AHM = 1/2 AH.HN = 1/2 .6.2,5 = 7,5cm²