Bài I.1, I.2 trang 166 SBT Toán 8 tập 1

Bài I.1, I.2 trang 166 SBT Toán 8 tập 1

Bài 1 trang 166 SBT Toán 8 Tập 1: Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, O, hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao.

Lời giải:

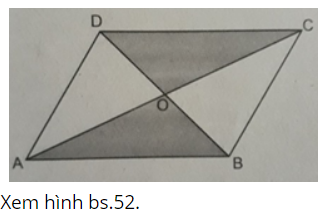
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.

- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.

Bài 2 trang 166 SBT Toán 8 Tập 1: Cho hình lục giác ABCDEF, có AB = BC = 3cm và ED = 4cm. Biết rằng ED song song với AB, AB vuông góc với BC, FE vuông góc với FA vuông góc với FA và FE = FA. Qua điểm A kẻ đường thẳng d song song với BC. Gọi K là giao điểm của d và ED, biết AK = 4cm, KD = 1cm. Tính diện tích của lục giác đó.

Mỗi bài từ số II.3 đến II.11 sau đây đều có bốn phương án lựa chọn là (A), (B), (C) và (D) nhưng chỉ có một trong số đó là đúng. Hãy chỉ ra phương án mà em cho là đúng.

Lời giải:

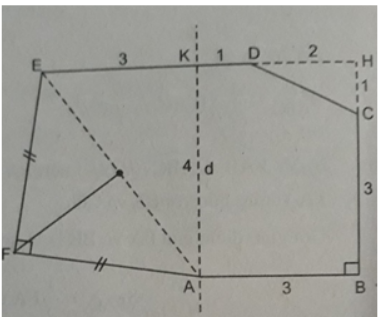
Gọi H là giao điểm của hai đường thẳng ED và BC. Khi đó, ABHE là hình thang và tính được diện tích của nó là

S₁ = 1/2 (AB + EH).BH = 1/2 (3 + 6).4 = 18( cm²).

Diện tích của tam giác vuông DHC là

S₂ = 1/2 DH.CH = 1/2.2.1 = 1( cm²).

Trong tam giác vuông AKE tính được EA = 5 (cm).

Trong tam giác vuông FEA có FE = FA suy ra EF2 = 25/2.

Từ đó diện tích của tam giác FAE là S₃ = 25/4 cm².

Vậy diện tích của lục giác đã cho là

S = S₃ + S₁ - S₂ = 25/4 + 18 – 1 = 93/4( cm²).