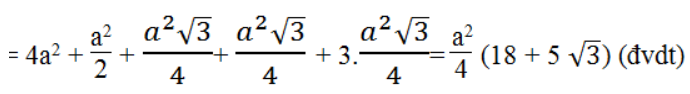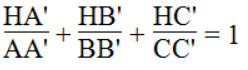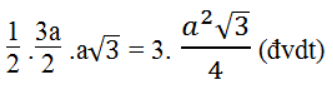Bài 51 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chứng minh rằng
Lời giải:
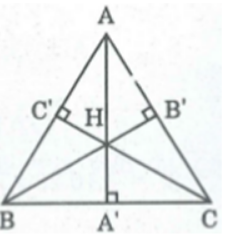
Ta có: SHBC + SHAC + SHAB = SABC
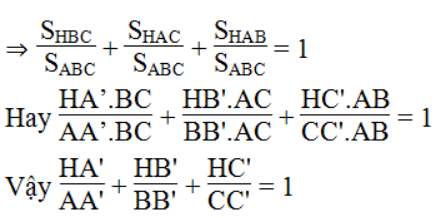
Bài 52 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC.
a. Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C
b. Tại sao nếu AB < AC thì BB' < CC’
Lời giải:
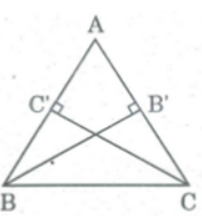
a. Ta có: SABC = BB'.AC2 = CC'.AB2
Suy ra: BB'.AC = CC'.AB
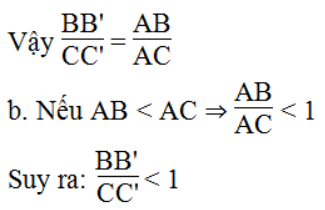
Vậy BB' < CC'.
Bài 53 trang 166 SBT Toán 8 Tập 1: Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thắng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo).
Lời giải:
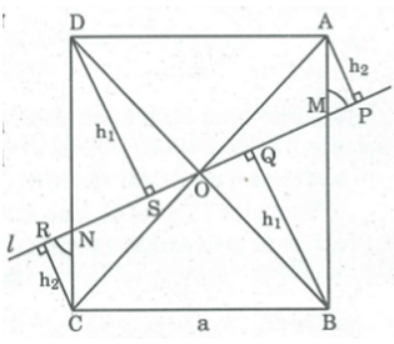
Gọi h1 và h2 là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l
Tổng khoảng cách là S.
Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)
Suy ra AM = CN
Mà: ∠(AMP) = ∠(DNS) (đồng vị)
∠(DNS) = ∠(CNR) (đôi đỉnh)
Suy ra: ∠(AMP) = ∠(CNR)
Suy ra: ΔAPM = ΔCRN (cạnh huyền, góc nhọn)
⇒ CR = AP = h2
AM = CD ⇒ BM = DN
∠(BMQ) = ∠(DNS) (so le trong)
Suy ra: ΔBQM = ΔDSN (cạnh huyền, góc nhọn) ⇒ DS = BQ = h1
SBOA = 1/4 SAOB = 1/4 a2 (l)
SBOA = SBOM + SAOM = 1/2 .b/2 .h1 + 1/2 .b/2 .h2
Từ (1) va (2) suy ra h1 + h2 = a2b . Vậy : S = 2(h1 + h2) = 2a2b
Bài 54 trang 166 SBT Toán 8 Tập 1: Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN.
Lời giải:
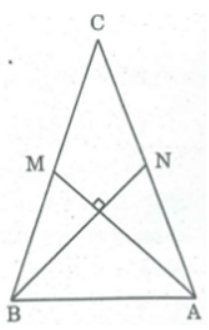
Tứ giác ẠBMN có hai đường chéo vuông góc.
Ta có: SABMN = 1/2 AM.BN
Δ ABM và Δ AMC có chung chiều cao kể từ A, cạnh đáy BM = MC nên: SABM = SAMC = 1/2 SABC
ΔMNA và ΔMNC có chung chiều cao kê từ M, cạnh đáy AN = NC nên: SMAN = SMNC = 1/2 SAMC = 1/4 SABC
SABMN = SABM + SMNA = 1/2 SABC + 1/4 SABC = 3/4 SABC
Vậy SABC = 4/3 SABMN = 4/3 .1/2 .AM.BN = 2/3 AM.BN
Bài 55 trang 166 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC. Tính tỉ số diện tích của:
a. Các tam giác DAC và DCK;
b. Tam giác DAc và tứ giác ADLB;
c. Các tứ giác ABKD và ABLD.
Lời giải:
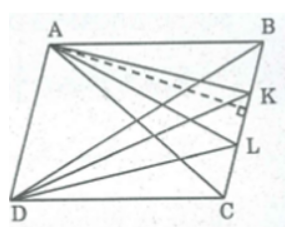
a. Ta có: SACD = SBCD = SDAB = SCAB = 1/2 SABCD (1)
ΔDCK và ΔDCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy CK = 2/3 CB
SDCK = 2/3 SDBC (2)
Từ (1) và (2)
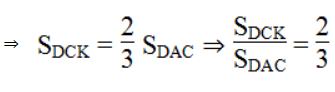
b. Ta có: SADLB = SADB + SDLB
ΔDBC và ΔDLB có chung chiều cao kẻ từ D, Cạnh đáy LB = 2/3 BC ⇒ SDLB = 2/3 SDBC
Mà SDAC = SADB = SDBC (chứng minh trên)
Suy ra: SADLB = SDAC + 2/3 SDAC = 5/3 SDAC
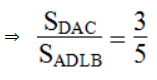
Ta có: SABKD = SABD + SDKB
ΔDKB và ΔDCB có chung chiều cao kể từ D, cạnh đáy BL = 1/3 BC
⇒ SDKB = 1/3 SDCB
Mà SDCB = SDAC = SABD (chứng minh trên)
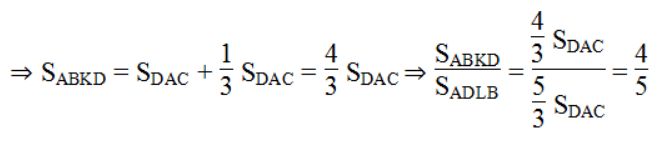
Bài 56 trang 166 SBT Toán 8 Tập 1: Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC.
a. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
b. Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.
c. Tính diện tích tứ giác DEFCL
Lời giải:
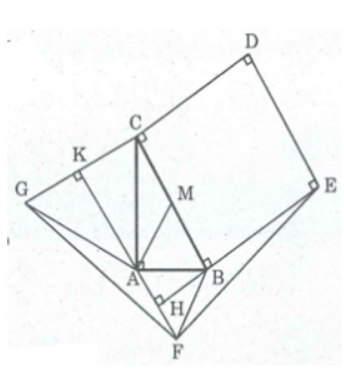
a. Gọi M là trung điểm của BG, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ΔAMB đều ⇒ ∠(ABC) = 60o
Mặt khác: ∠(ABC) = ∠(ACB) (tính chất tam giác vuông)
Suy ra: ∠(ACB) = 90o - ∠(ABC) = 90o – 60o = 30o
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: BC2 = AB2+ AC2
⇒ AC2 = BC2 - AB2 = 4a2 - a2 = 3a2 ⇒ AC = a√3
Vậy SABC = 1/2 .AB.AC
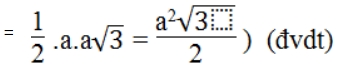
b. Ta có: ∠(FAB) = ∠(ABC) = 60o
FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
BC ⊥ BE (vì BCDE là hình vuông)
Suy ra: FA ⊥ BE
BC ⊥ CD (vì BCDE là hình vuông)
Suy ra: FA ⊥ CD
Gọi giao điểm BE và FA là H, FA và CG là K.
⇒ BH ⊥ FA và FH = HA = a2 (tính chất tam giác đều)
∠(ACG) + ∠(ACB) + ∠(BCD) = 60o + 30o + 90o = 180o
⇒ G, C, D thẳng hàng
⇒ AK ⊥ CG và GK = KC = 1/2 GC = 1/2 AC = (a√3)/2
SFAG = 1/2 GK.AF =
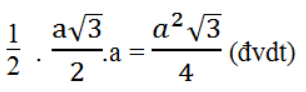
SFBE = 1/2 FH.BE = 1/2 .a2 .2a = 1/2 a2 (đvdt)
c. SBCDE = BC2 = (2a)2 = 4a2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: AH2 + BH2 = AB2
⇒ BH2 = AB2 - AH2 = a2 - a24 = 3a24 ⇒ BH = (a√3)/2
SABF = 1/2 BH.FA = 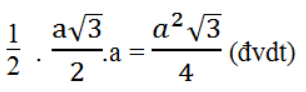
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: AC2 = AK2 + KC2
⇒ AK2 = AC2 - KC2 = 3a2 - 3a24 = 9a24 ⇒ AK = 3a2 (đvdt)
SACG = 1/2 AK.CG =
SDEFG = SBCDE + SFBE + SFAB + SFAG + SACG