Bài 3.1, 3.2 trang 89 SBT Toán 8 tập 2
Bài 3.1, 3.2 trang 89 SBT Toán 8 tập 2
Bài 3.1 trang 89 sách bài tập Toán 8 Tập 2: Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm
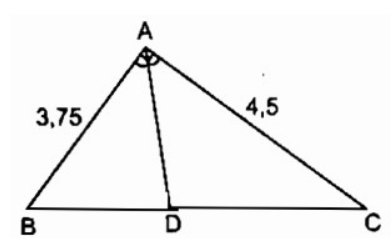
Hãy chọn kết quả đúng (tính chính xác đến chữ số thập phân).
1. Độ dài của đoạn thẳng BD là:
A. 18,58
B. 2,66
C. 2,65
D. 3,25
2. Độ dài đoạn thẳng CD là:
A. 27,13
B. 2,68
C. 3,2
D. 3,15
Lời giải:
1. Chọn B
2. Chọn C
Bài 3.2 trang 89 sách bài tập Toán 8 Tập 2: Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F.
Hãy tính độ dài đường chéo AC, biết EF = m = 3,45cm.
(Tính chính xác đến hai chữ số thập phân)

Lời giải:
Vì ABCD là hình bình hành nên ∠ABC = ∠ADC.
Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra ∠ADF = ∠CBE
Mặt khác, ta có: AD = CB = b;
∠DAF = ∠BCE (so le trong)
Suy ra: ΔADF = ΔCBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có:
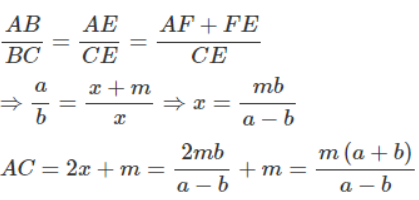
Thay số, tính trên máy tính điện tử cầm tay ta được: