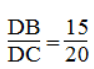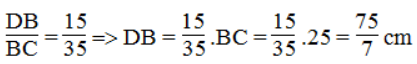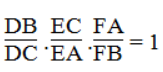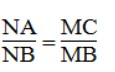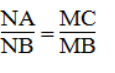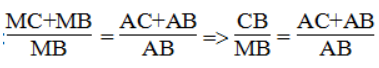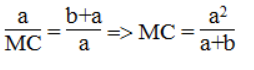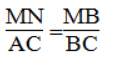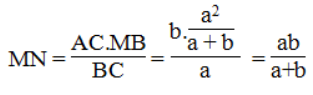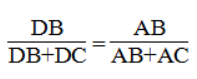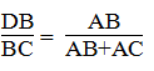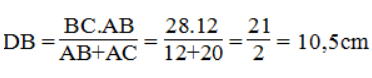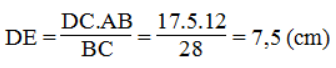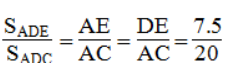(SGK + SBT) Giải Toán 8 trang 87 Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 87 Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 87.
(SGK + SBT) Giải Toán 8 trang 87 Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 87 Tập 1 (sách mới):
- Toán lớp 8 trang 87 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 87 (sách cũ)
Bài 17 trang 87 sách bài tập Toán 8 Tập 2: Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D.
a. Tính độ dài các đoạn thẳng DB và DC.
b. Tính tỉ số diện tích của hai tam giác ABD và ACD.
Lời giải:
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: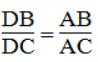 
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên 
Suy ra: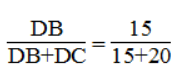 
(tính chất tỉ lệ thức)
Suy ra: 
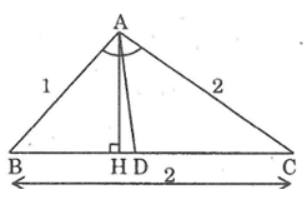
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
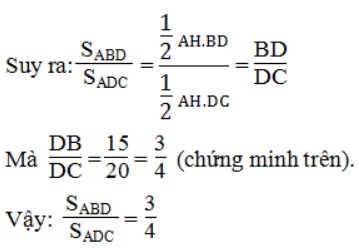
Bài 18 trang 87 sách bài tập Toán 8 Tập 2: Tam giác ABC có các đường phân giác AD,BE,CF
Chứng minh rằng: 
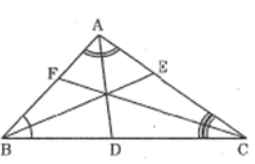
Lời giải:
Trong ΔABC, ta có: AD là đường phân giác của ∠(BAC)
Suy ra: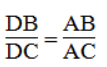 
(tính chất đường phân giác) (1)
BE là đường phân giác của ∠(ABC)
Suy ra: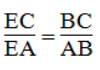 
(tỉnh chất đường phân giác) (2)
CF là đường phân giác của ∠(ACB)
Suy ra: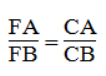 
(tính chất đường phân giác) (3)
Nhân từng vế (1), (2) và (3) ta có:
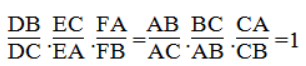
Bài 19 trang 87 sách bài tập Toán 8 Tập 2: Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N.
a. Chứng minh MN // AC
b. Tính MN theo a, b.
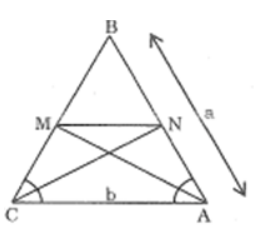
Lời giải:
a. Trong ΔBAC, ta có: AM là đường phân giác của (BAC)
Suy ra: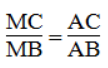 
(tỉnh chất đường phân giác) (1)
CN là đường phân giác của (BCA)
Suy ra: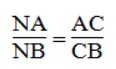 
(tỉnh chất đường phân giác) (2)
Lại có: AB = CB = a (gt)
Từ (1), (2) và (gt) suy ra: 
Trong ΔBAC, ta có: 
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).
Ta có: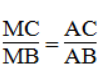 
(chứng minh trên)
Suy ra: 
Hay 
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và 
Vậy 
Bài 20 trang 87 sách bài tập Toán 8 Tập 2: Tam giác ABC có AB= 12cm, AC = 20cm, BC= 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ BC).
a. Tính độ dài các đoạn thẳng BD, DC, DE.
b. Cho biết diện tích tam giác ABC là S,tính diện tích các tam ABD, ADC, DCE
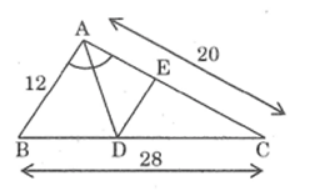
Lời giải:
a. * Trong ΔABC, ta có:
AD là đường phân giác của ∠(BAC)
Suy ra: 
(tính chất tia phân giác)
Suy ra: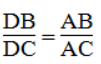 
Suy ra: 
Suy ra: 
Vậy DC = BC - DB = 28 - 10,5 = 17,5 (cm)
* Trong ΔABC, ta có: DE // AB
Suy ra: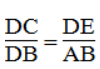 
(Hệ quả định lí Ta-lét)
Vậy: 
b. Vì ΔABD và ΔABC có chung đường cao kẻ từ đỉnh A nên:
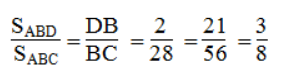
Vậy: SABD = 3/8.S
SADC = SABC - SABD = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: 
Vậy: SADE = 7,5/20 SADC = 7,5/20 . 5/8.S = 7,5/32.S
Ta có: SDCE = SADC - SADE = 5/8.S - 7,5/32.S = 12,5/32.S
