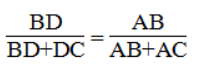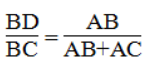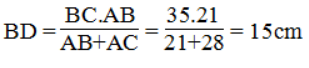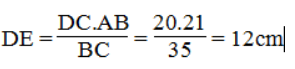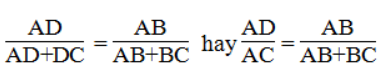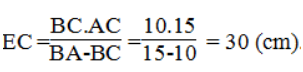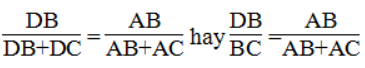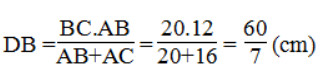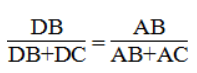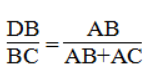Bài 21, 22, 23, 24 trang 88 SBT Toán 8 tập 2

---

Bài 21, 22, 23, 24 trang 88 SBT Toán 8 tập 2

Bài 21 trang 88 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E.

a. Tính dộ dài các đoạn thẳng BD,DC và DE.

b. Tính diện tích tam giác ABD và diện tich tam giác ACD.

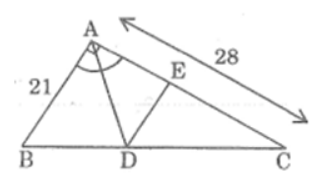
Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 21² + 28² = 1225

Suy ra: BC = 35 (cm)

Vì AD là đường phân giác của ∠(BAC) nên:

(t/chất đường phân giác)

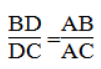
Suy ra:

Hay

Suy ra:

Vậy DC = BC – BD = 35 – 15 = 20cm

Trong ΔABC ta có: DE // AB

Suy ra: 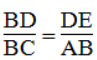(Hệ quả định lí Ta-lét)

Suy ra:

b. Ta có: S_ABC = 1/2.AB.AC = 1/2.21.28 = 294 (cm²)

Vì ΔABC và ΔADB có chung đường cao kẻ từ đỉnh A nên:

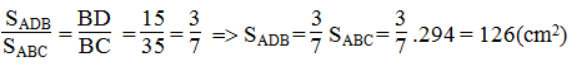
Vậy S_ADC = S_ABC – S_ABD = 294 – 126 = 168(cm²)

Bài 22 trang 88 sách bài tập Toán 8 Tập 2: Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.

a. Tính AD, DC.

b. Đường vuông góc với BD tại B cắt đường thẳng AC tại E. Tính EC.

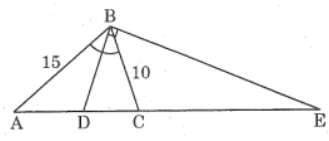
Lời giải:

Vì BD là đường phân giác của ∠(ABC) nên:

(t/chất đường phân giác)

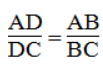
Suy ra:

Mà ΔABC cân tại A nên AC = AB = 15 (cm)

Suy ra: AD/15 = 15/(15+10) ⇒ AD = (15.15)/25 = 9(cm)

Vậy DC = AC – AD = 15 – 9 = 6 (cm)

b. Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B

Suy ra : 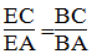( t/chất đường phân giác)

Suy ra: ⇒ EC.BA= BC (EC + AC)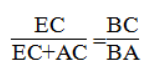

Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC

Vậy

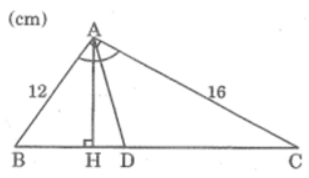
Bài 23 trang 88 sách bài tập Toán 8 Tập 2: Tam giác ABC có góc A = 90^o, AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D.

a. Tính BC, BD và DC.

b. Kẻ đường cao AH, tỉnh AH, HD và AD.

(t/chất đường phân giác)

Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 12² + 16² = 400

Suy ra: BC =20 (cm)

Vì AD là đường phân giác của ∠(BAC) nên:

(tỉnh chất đường phân giác)

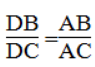
Suy ra:

Suy ra:

Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)

b. Ta có: SABC =1/2.AB.AC = 1/2.AH.BC

Suy ra: AB.AC = AH.BC

(t/chất đường phân giác)

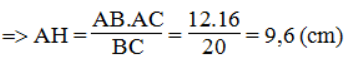
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90^o

Theo định lí Pi-ta-go, ta có: AB² = AH² + HB²

Suy ra: HB² = AB² - AH² = 12² - (9,6)² = 51,84 ⇒ HB =7,2 (cm)

Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)

Trong tam giác vuông AHD, ta có: ∠(AHD) = 90^o

Theo định lí Pi-ta-go, ta có:

AD² = AH² + HD² = (9,6)² + (1,37)² = 94,0369

Suy ra: AD ≈ 9,70 (cm)

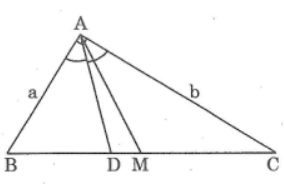
Bài 24 trang 88 sách bài tập Toán 8 Tập 2: Tam giác ABC có ∠A = 90°, AB = a (cm), AC = b (cm) (a < b), trung tuyến AM, dường phân giác AD (M và D thuộc cạnh BC)

a. Tính độ dài các đoạn thẳng BD, DC, AM và DM theo a, b

b. Hãy tính độ dài các đoạn thẳng trên chính xác đên chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.

(t/chất đường phân giác)

Lời giải:

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = a² + b²

Suy ra: BC = a² + b²

Ta có: AM = BM = 1/2.BC (tính chất tam giác vuông).

Suy ra: AM = 1/2 √(a₂ + b₂)

Vì AD là đường phân giác của ∠(BAC) nên:

(tính chất đường phân giác)

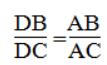
Suy ra:

hay

(t/chất đường phân giác)

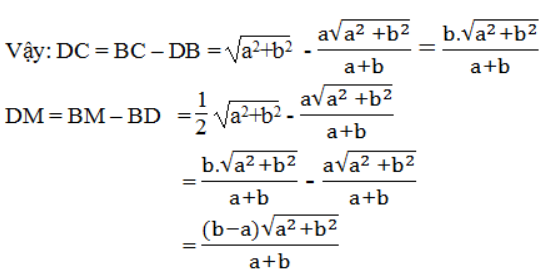
b. Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tỉnh, ta tính được:

DC ≈ 5,31 cm

AM ≈ 4,18 cm

DM ≈ 1,14cm