Bài 22, 23 trang 82 SBT Toán 8 tập 1
Bài 22, 23 trang 82 SBT Toán 8 tập 1
Bài 22 trang 82 SBT Toán 8 Tập 1: Hình thang cân ABCD có AB //CD, AB > CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DC = CK
Lời giải:
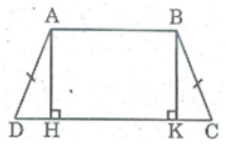
Xét hai tam giác vuông AHD và BKC:
∠(AHD) = ∠(BKC) = 90o
AD = BC (tính chất hình thang cân)
∠C = ∠D (gt)
Suy ra: ΔAHD = ΔBKC (cạnh huyền, góc nhọn)
⇒ HD = KC
Bài 23 trang 82 SBT Toán 8 Tập 1: Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.
Lời giải:
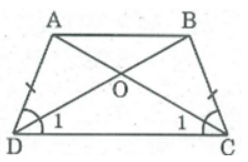
Xét ΔADC và ΔBCD, ta có:
AD = BC (tính chất hình thang cân)
∠(ADC) = ∠(BCD) (gt)
DC chung
Do đó: ΔADC = ΔBCD (c.g.c) ⇒ ∠C1= ∠D1
Trong ΔOCD ta có: ∠C1= ∠D1 ⇒ ΔOCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.

