(SGK + SBT) Giải Toán 8 trang 53 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 53 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 53.
(SGK + SBT) Giải Toán 8 trang 53 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 53 Tập 1 (sách mới):
- Toán lớp 8 trang 53 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 53 (sách cũ)
Bài 23 trang 53 sách bài tập Toán 8 Tập 2: Cho a > 0, b > 0 và a > b, chứng tỏ 1a < 1b
Lời giải:
Ta có: a > 0, b > 0⇒ a.b > 0.b⇒ ab > 0⇒ 1/ab > 0
a > b⇒ a. 1/ab > b. 1/ab⇒ 1/b > 1/a⇒ 1/a < 1/b
Bài 24 trang 53 sách bài tập Toán 8 Tập 2: Điền dấu >, < vào ô vuông cho thích hợp:
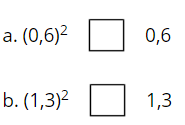
Lời giải:

Bài 25 trang 53 sách bài tập Toán 8 Tập 2: So sánh m2 và m nếu:
a. m lớn hơn 1
b. m dương nhưng nhỏ hơn 1
Lời giải:
a. Ta có: m > 1 ⇒ m.m > 1.m ⇒ m2 > m
b. Ta có: m> 0 và m < 1 ⇒ m.m < 1.m ⇒ m2 < m
Bài 26 trang 53 sách bài tập Toán 8 Tập 2: Cho a < b và c < d, chứng tỏ a + c < b + d
Lời giải:
Ta có: a < b ⇒ a + c < b + c (1)
c < d ⇒ b + c < b + d (2)
Từ (1) và (2) suy ra: a + c < b + d.
Bài 27 trang 53 sách bài tập Toán 8 Tập 2: Cho a, b, c, d là các số dương thỏa mãn a < b, c < d, chứng tỏ ac < bd.
Lời giải:
Với a > 0, b > 0, c > 0, d > 0 ta có:
a < b ⇒ ac < bc (1)
c < d ⇒ bc < bd (2)
Từ (1) và (2) suy ra: ac < bd.
Bài 28 trang 53 sách bài tập Toán 8 Tập 2: Chứng tỏ rằng với a và b là các số bất kì thì:
a. a2 + b2 – 2ab ≥ 0
b. (a2 + b2)/2 ≥ ab
Lời giải:
a. Ta có: (a – b)2 ≥ 0 ⇒ a2 + b2 – 2ab ≥ 0
b. Ta có: (a – b)2 ≥ 0 ⇒ a2 + b2 – 2ab ≥ 0
⇒ a2 + b2 – 2ab + 2ab ≥ 2ab ⇒ a2 + b2 ≥ 2ab
⇒ (a2 + b2). 1/2 ≥ 2ab. 1/2 ⇒ (a2 + b2)/2 ≥ ab
Bài 29 trang 53 sách bài tập Toán 8 Tập 2: Cho a và b là các số dương, chứng tỏ: a/b + b/a ≥ 2.
Lời giải:
Ta có: (a – b)2 ≥ 0 ⇒ a2 + b2 – 2ab ≥ 0
⇒ a2 + b2 – 2ab + 2ab ≥ 2ab ⇒ a2 + b2 ≥ 2ab (*)
a > 0, b > 0 ⇒ a.b > 0 ⇒ 1/ab > 0
Nhân hai vế của (*) với 1/ab ta có:
(a2 + b2). 1/ab ≥ 2/ab. 1/ab ⇔ a2/ab + b2/ab ≥ 2 ⇔ a/b + b/a ≥ 2
Bài 30 trang 53 sách bài tập Toán 8 Tập 2: a. Với số a bất kì, chứng tỏ: a(a + 2) < (a + 1)2
b. Chứng minh rằng: Trong ba số nguyên liên tiếp thì bình phương số đứng giữa lớn hơn tích hai số còn lại.
Lời giải:
a. Ta có: 0 < 1 ⇒ a2 + 2a + 0 < a2 + 2a + 1 ⇒ a2 + 2a < (a + 1)2
⇒ a(a + 2) < (a + 1)2
b. Gọi a, a + 1, a + 2 là ba số nguyên liên tiếp, ta có:
(a + 1)2 = a2 + 2a + 1 (1)
a(a + 2) = a2 + 2a (2)
Từ (1) và (2) suy ra: a(a + 2) < (a + 1)2.
Vậy trong ba số nguyên liên tiếp thì bình phương số đứng giữa lớn hơn tích hai số còn lại.

