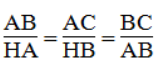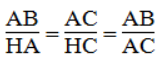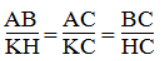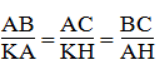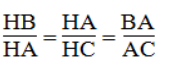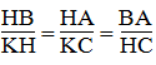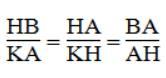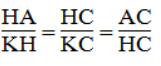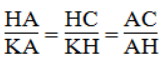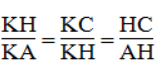Bài 39, 40 trang 93 SBT Toán 8 tập 2

---

Bài 39, 40 trang 93 SBT Toán 8 tập 2

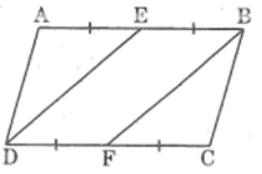
Bài 39 trang 93 sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD .Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh hai tam giác ADE và CBF đồng dạng với nhau.

Lời giải:

Vì ABCD là hình bình hành nên:

AB = CD (1)

Theo giả thiết:

AE = EB = 1/2 AB (2)

DF = FC = 1/2 CD (3)

Từ (1), (2) và (3) suy ra:

EB = DF và BE // DF.

Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)

Suy ra: DE // BF

Ta có: ∠(AED) =∠(ABF ) (đồng vị)

∠(ABF) = ∠(BFC) (so le trong)

Suy ra: ∠(AED) = ∠( BFC)

Xét ΔAED'và ΔCFB ta có:

∠(AED) =∠( BFC) (chứng minh trên)

∠A = ∠C (tính chất hình bình hành)

Vậy: ΔAED đồng dạng ΔCFB (g.g)

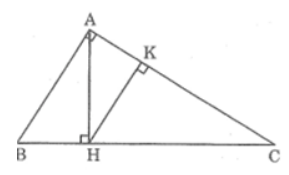
Bài 40 trang 93 sách bài tập Toán 8 Tập 2: Tam giác vuông ABC có ∠A = 90° và đường cao AH. Từ H hạ HK vuông góc vói AC

a. Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

b. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.

Lời giải:

a. Trong hình trên có 5 tam giác đồng dạng với nhau theo từng đôi một đó là:

ΔABC; ΔHAB; ΔHAC; ΔKAH; ΔKHC.

b. Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:

- ΔABC đồng dạng ΔHAB. Ta có:

- ΔABC đồng dạng ΔHAC. Ta có:

- ΔABC đồngdạng ΔKHC. Ta có:

- ΔABC đồng dạng ΔKAH. Ta có:

- ΔHBA đồng dạng ΔHAC. Ta có:

- ΔHBA đồng dạng ΔKHC. Ta có:

- ΔHBA đồng dạng ΔKAH. Ta có:

- ΔHAC đồng dạng ΔKHC.Ta có:

- ΔHAC đồng dạng ΔKAH. Ta có:

- ΔKHC đồngdạng ΔKAH. Ta có: