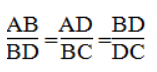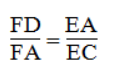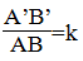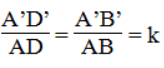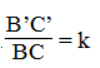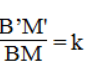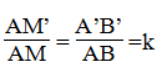Bài 41, 42, 43 trang 94 SBT Toán 8 tập 2

---

Bài 41, 42, 43 trang 94 SBT Toán 8 tập 2

Bài 41 trang 94 sách bài tập Toán 8 Tập 2: Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠(DAB) = ∠(DBC)

a. Chứng minh tam giác ADB đồng dạng với tam giác BCD.

b. Tính độ dài BC, CD

c. Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.

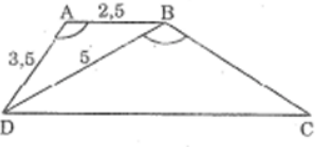
Lời giải:

a.Xét ΔABD và ΔBDC, ta có:

∠(DAB) = ∠(DBC) (gt)

∠(ABD) = ∠(BDC) (so le trong)

Suy ra: ΔABD ∼ ΔBDC (g.g)

b. Vì ΔABD ∼ ΔBDC nên:

Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:

⇒BC=(5.4.5)/(2.5) = 7(cm)

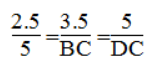
Vậy DC = (5.5)/(2.5) = 10(cm)

Bài 42 trang 94 sách bài tập Toán 8 Tập 2: Cho tam giác vuông ABC có ∠A = 90o .Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F.

Chứng minh:

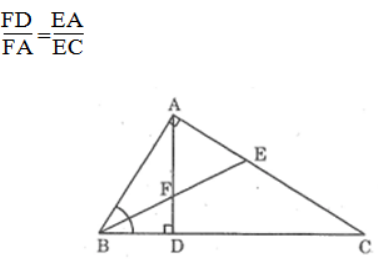
Lời giải:

Trong ΔABC, ta có BE là tia phân giác của ∠(ABC)

Suy ra: 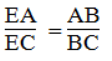(tính chất đường phân giác) (1)

Trong ΔADB, ta có BF là tia phân giác của ∠(ABD)

Suy ra: 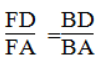(tính chất đường phân giác) (2)

Xét ΔABC và ΔDAB, ta có:

∠(BAC) =∠(BDA) = 90^o

Góc B chung

Suy ra: ΔABC đồng dạng ΔDBA (g.g)

Suy ra: 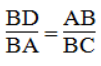(3)

Từ (1), (2) và (3) Suy ra:

Bài 43 trang 94 sách bài tập Toán 8 Tập 2: Chứng minh rằng nếu haị tam giác ABC và đồng dạng A'B'C' với nhau thì:

a. Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng

b. Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng

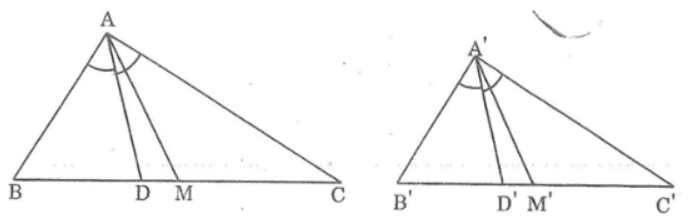
Lời giải:

Vì ΔABC đồng dạng ΔA'B'C' nên ta có:

∠A =∠(A') ; ∠B = ∠(B') và

Lại có: ∠(BAD) = 1/2 ∠A (gt) và ∠(B'A'D') = 1/2 ∠(A') (gt)

Suy ra: (BAD) = (B'A'D')

Xét ΔABD và ΔA'B'D' ta có:

∠B = ∠(B') (chứng minh trên)

∠(BAD) = ∠(B'A'D') (chứng minh trên)

Suy ra: ΔABD đồng dạng ΔA'B'D' (g.g)

Vậy :

Vì ΔABC đồng dạng ΔA'B'C' nên

Mà B'M' =1/2 B'C' và BM =1/2 BC nên

Xét ΔABM và ΔA'B'M', ta có:

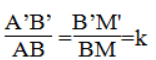
B = (B') (chứng minh trên)

Suy ra: ΔABM đồng dạng ΔA'B'M' (c.g.c)

Vậy: