(SGK + SBT) Giải Toán 8 trang 14 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 14 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 14.
(SGK + SBT) Giải Toán 8 trang 14 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 14 Tập 1 (sách mới):
- Toán lớp 8 trang 14 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 14 (sách cũ)
Bài 54 trang 14 SBT Toán 8 Tập 1: Làm tính nhân:
a. (x2 – 1)(x2 + 2x)
b. (x + 3y)(x2 – 2xy + y)
c. (2x – 1)(3x + 2)(3 – x)
Lời giải:
a. (x2 – 1)(x2 + 2x)
= x4 + 2x3 – x2 – 2x
b. (x + 3y)(x2 – 2xy + y)
= x3 – 2x2y + xy + 3x2y – 6xy2 + 3y2
= x3 + x2y + xy – 6xy2 + 3y2
c. (2x – 1)(3x + 2)(3 – x)
= (6x2 + 4x – 3x – 2)(3 – x)
= (6x2 + x – 2)(3 – x)
= 18x2 – 6x3 + 3x – x2 – 6 + 2x
= 17x2 – 6x3 + 5x – 6
Bài 55 trang 14 SBT Toán 8 Tập 1: Tính nhanh giá trị của mỗi biểu thức sau:
a. 1,62 + 4.0,8.3,4 + 3,42
b. 34.54 – (152 + 1)(152 – 1)
c. x4 – 12x3 + 12x2 – 12x + 111 tại x = 11
Lời giải:
a. 1,62 + 4.0,8.3,4 + 3,42
= 1,62 + 2.1,6.3,4 + 3,42
= (1,6 + 3,4)2 = 52 = 25
b. 34.54 – (152 + 1)(152 – 1)
= (3.5)4 – (154 – 1)
= 154 - 154 + 1 = 1
c. Với x = 11, ta có: 12 = x + 1
Suy ra: x4 – 12x3 + 12x2 – 12x + 111
= x4 – (x + 1)x3 + (x + 1)x2 – (x + 1)x + 111
= x4 - x4 - x3 + x3 + x2 - x2 – x + 111 = - x + 111
Thay x = 11 vào biểu thức ta được: - x + 111 = - 11 + 111 = 100
Bài 56 trang 14 SBT Toán 8 Tập 1: Rút gọn biểu thức:
a. (6x + 1)2 + (6x – 1)2 – 2(1 + 6x)(6x – 1)
b. 3(22 + 1)(24 + 1)(28 + 1)(216 + 1)
Lời giải:
a. (6x + 1)2 + (6x – 1)2 – 2(1 + 6x)(6x – 1)
= (6x + 1)2 – 2(1 + 6x)(6x – 1) + (6x – 1)2
= [(6x + 1) – (6x – 1)]2
= (6x + 1 – 6x + 1)2 = 22 = 4
b. 3(22 + 1)(24 + 1)(28 + 1)(216 + 1)
= (22 – 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
= (24 - 1)(24 + 1)(28 + 1)(216 + 1)
= (28 - 1)(28 + 1)(216 + 1)
= (216 - 1)(216 + 1)
= 232 – 1
Bài 57 trang 14 SBT Toán 8 Tập 1: Phân tích đa thức thành nhân tử:
a. x3 – 3x2 – 4x + 12
b. x4 – 5x2 + 4
c. (x + y + z)3 – x3 – y3 – z3
Lời giải:
a. x3 – 3x2 – 4x + 12
= (x3 – 3x2 ) – (4x – 12)
= x2(x – 3) – 4(x – 3)
= (x – 3)(x2 – 4)
= (x – 3)(x + 2)(x – 2)
b. x4 – 5x2 + 4
= x4 – 4x2 - x2 + 4
= (x4 – 4x2 ) – (x2 - 4)
= x2(x2 – 4) – (x2 – 4)
= (x2 – 4)( x2 – 1)
= (x + 2)(x – 2)(x + 1)(x – 1)
c. (x + y + z)3 – x3 – y3 – z3
= [(x + y) + z]3 – x3 – y3 – z3
= (x + y)3 + 3(x + y)2z + 3(x + y)z2 + – x3 – y3 – z3
= x3 + y3 + 3xy(x + y) + 3(x + y)2z + 3(x + y)z2 – x3 – y3
= 3(x + y)[xy + (x + y)z + z2]
= 3(x + y)[xy + xz + yz + z2]
= 3(x + y)[x(y + z) + z(y + z)]
= 3(x + y)(y + z)(x + z)
Bài 58 trang 14 SBT Toán 8 Tập 1: Làm phép chia:
a. (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1)
b. (2x3 - 5x2 + 6x – 15) : (2x – 5)
c. (x4 – x – 14) : (x – 2)
Lời giải:
a
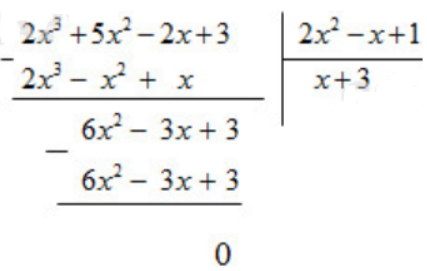
b
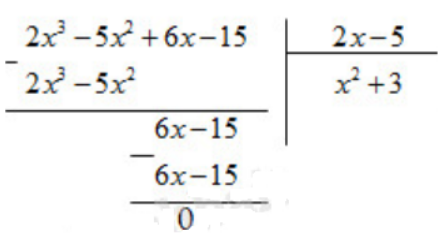
c
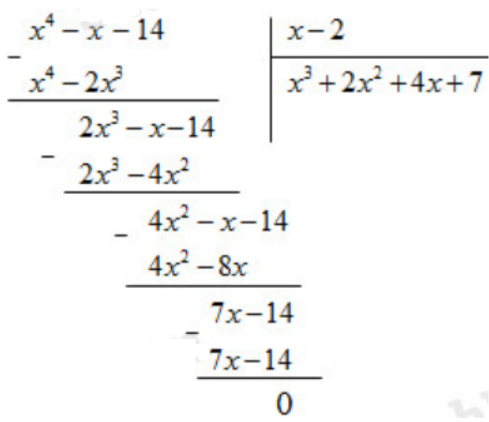
Bài 59 trang 14 SBT Toán 8 Tập 1: Tìm giá trị lớn nhất (hoặc nhỏ nhất) của các biểu thức sau:
a. A = x2 – 6x + 11
b. B = 2x2 + 10x – 1
c. C = 5x – x2
Lời giải:
a. Ta có: A = x2 – 6x + 11 = x2 – 2.3x + 9 + 2 = (x – 3)2 + 2
Vì (x – 3)2 ≤ 0 nên (x – 3)2 + 2 ≤ 2
Suy ra: A ≤ 2.
Vậy A = 2 là giá trị nhỏ nhất của biểu thức tại x = 3.
b. B = 2x2 + 10x – 1 = 2(x2 + 5x - 1/2 )
= 2[x2 + 2.5/2 x + (5/2 )2 – (5/2 )2 - 1/2 ]
= 2[(x + 5/2 )2 - 25/4 - 2/4 ] = 2[(x + 5/2 )2 - 27/4 ] = 2(x + 5/2)2 - 27/2
Vì (x + 5/2 )2 ≤ 0 nên 2(x + 5/2 )2 ≤ 0 ⇒ 2(x + 5/2 )2 - 27/2 ≤ - 27/2
Suy ra: B ≤ - 27/2 . Vậy B = 27/2 là giá trị nhỏ nhất tại x = - 5/2
c. C = 5x – x2 = -(x2 – 5x) = - [x2 - 2.5/2 x + (5/2 )2 – (5/2 )2]
= - [(x - 5/2 )2 - 25/4 ] = - (x - 5/2 )2 + 25/4
Vì (x - 5/2 )2 ≤ 0 nên - (x - 5/2 )2 ≥ 0 ⇒ - (x - 5/2 )2 + 25/4 ≥ 25/4
Suy ra: C ≥ 25/4 . Vậy C = 25/4 là giá trị lớn nhất tại x = 5/2 .

