Giải Toán 8 trang 14 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 14 Tập 1 trong Bài 2: Các phép toán với đa thức nhiều biến Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 14.

Giải Toán 8 trang 14 Tập 1 Chân trời sáng tạo

Thực hành 2 trang 14 Toán 8 Tập 1: Thực hiện các phép nhân đơn thức sau:

a) (4x³).(–6x³y);

b) (–2y).(–5xy²);

c) (–2a)³.(2ab)².

Lời giải:

a) (4x³).(–6x³y)

= [4.(–6)].(x³.x³).y

= –24x⁶y.

b) (–2y).(–5xy²)

= [(–2).(–5)].x.(y.y²)

= 10xy³.

c) (–2a)³.(2ab)²

= (–2)³.a³.2².a².b²

= [(–2)³.2²].(a³.a²).b²

= [(–8).4].a⁵b²

= –32a⁵b².

Khám phá 3 trang 14 Toán 8 Tập 1:

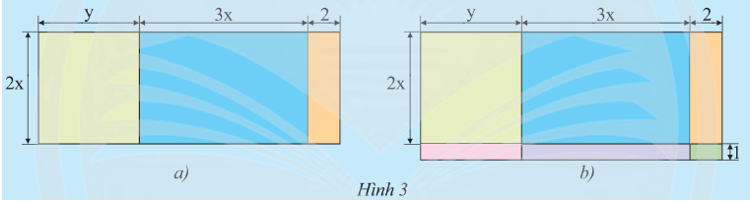
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.

b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.

Lời giải:

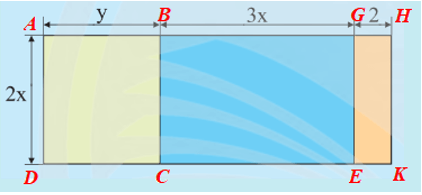
a) Cách 1: Chia sàn căn hộ thành ba hình chữ nhật ABCD, BCEG, EGHK (hình vẽ dưới đây), khi đó diện tích sàn căn hộ là tổng diện tích các hình chữ nhật trên.

Diện tích hình chữ nhật ABCD là: 2xy (m²).

Diện tích hình chữ nhật BCEG là: 2x.3x = 6x² (m²).

Diện tích hình chữ nhật EGHK là: 2x.2 = 4x (m²).

Diện tích sàn của căn hộ là: 2xy + 6x² + 4x (m²).

Cách 2: Tính chiều dài của sàn căn hộ rồi tính diện tích sàn căn hộ.

Chiều dài sàn của căn hộ là: y + 3x + 2 (m).

Diện tích sàn của căn hộ là: 2x.(y + 3x + 2) (m²).

Lưu ý: Ngoài 2 cách trên, có thể dùng cách khác để tính diện tích sàn của căn hộ.

b) Chiều rộng sàn của căn hộ (bao gồm cả ban công) là: 2x + 1 (m).

Diện tích sàn của căn hộ (bao gồm cả ban công) là: (2x + 1).(y + 3x + 2) (m²).

Lời giải bài tập Toán 8 Bài 2: Các phép toán với đa thức nhiều biến Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 12

• Giải Toán 8 trang 13

• Giải Toán 8 trang 15

• Giải Toán 8 trang 16

• Giải Toán 8 trang 17