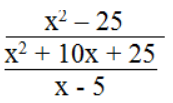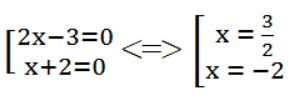(SGK + SBT) Giải Toán 8 trang 40 Chân trời sáng tạo

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 40 Chân trời sáng tạo sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 40.

(SGK + SBT) Giải Toán 8 trang 40 Chân trời sáng tạo

- Toán lớp 8 trang 40 Tập 1 (sách mới):

• Giải Toán 8 trang 40 Chân trời sáng tạo

  Xem lời giải

- Toán lớp 8 trang 40 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 40 (sách cũ)

Bài 59 trang 40 SBT Toán 8 Tập 1: Chứng minh đẳng thức:

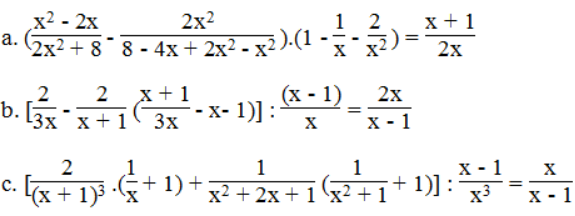
Lời giải:

a. Ta có:

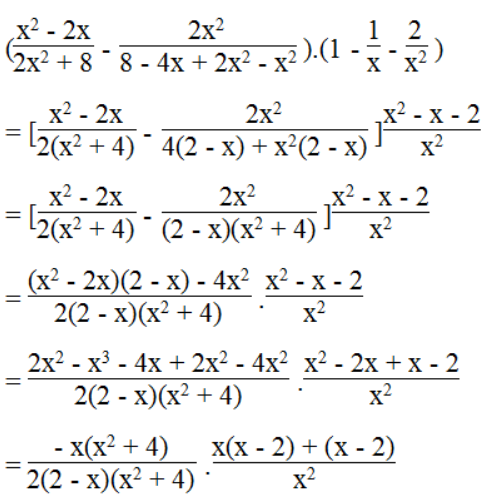
Vế trái bằng vế phải nên đẳng thức được chứng minh.

b. Ta có:

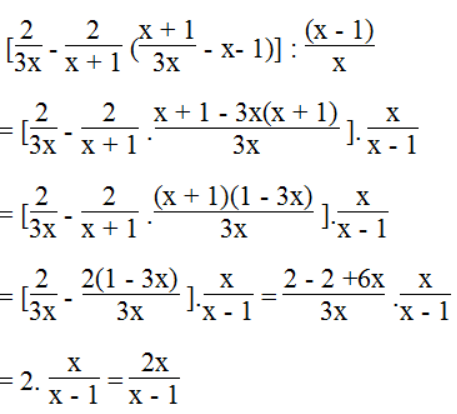
Vế trái bằng vế phải nên đẳng thức được chứng minh.

c. Ta có:

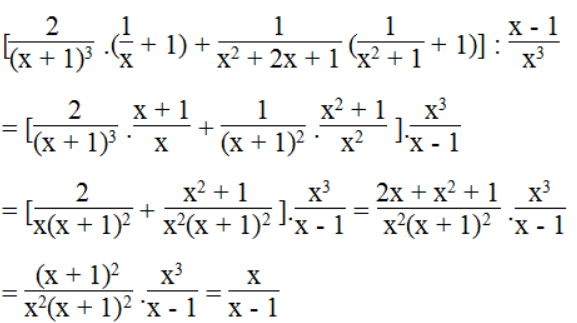
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Bài 60 trang 40 SBT Toán 8 Tập 1: Biến đổi các biểu thức hữu tỉ thành phân thức:

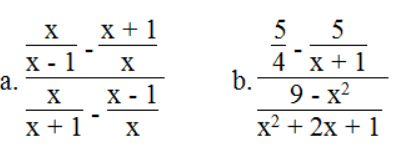
Lời giải:

a.

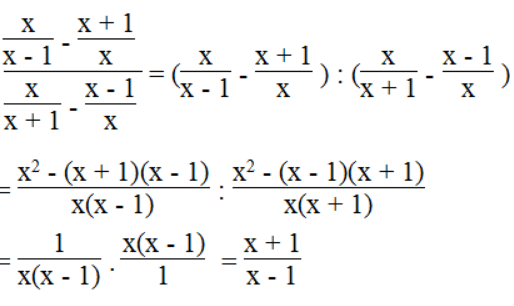
b.

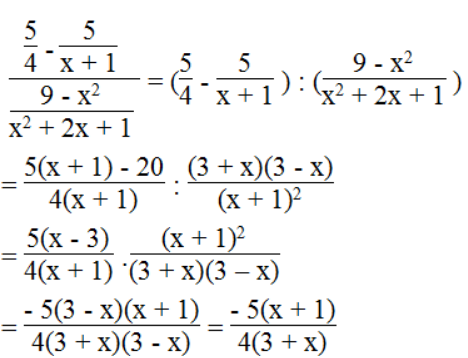
Bài 61 trang 40 SBT Toán 8 Tập 1: Một phân thức có giá trị bằng 0 khi giá trị của tử thức khác 0. Với giá trị nào của x thì các phân thức sau có giá trị bằng 0?

a.

b.

Lời giải:

a. Phân thức 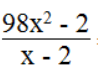= 0 khi 98x² – 2 = 0 và x – 2 ≠ 0

Ta có: x – 2 ≠ 0 ⇔ x ≠ 2

98x² – 2 = 0 ⇔ 2(49x² – 1) = 0 ⇔ (7x + 1)(7x – 1) = 0

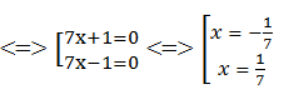
Ta có: x = 17 và x = - 17 thỏa mãn điều kiện x ≠ 2

Vậy x = 17 và x = - 17 thì phân thức 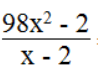có giá trị bằng 0.

b. Phân thức 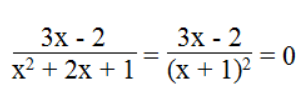khi 3x – 2 = 0 và (x+1)² ≠ 0

Ta có: (x+1)² ≠ 0 ⇔ x+1 ≠ 0 ⇔ x ≠ - 1

3x – 2 = 0 ⇔ x = 3/2

Ta có: x = 3/2 thỏa mãn điều kiện x ≠ - 1

Vậy x = 3/2 thì phân thức 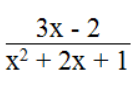có giá trị bằng 0.

Bài 62 trang 40 SBT Toán 8 Tập 1: Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định:

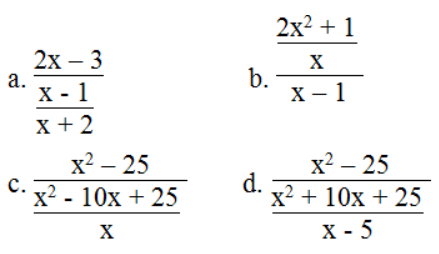
Lời giải:

a. Biểu thức 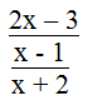xác định khi:

x – 1 ≠ 0 và x + 2 ≠ 0 ⇔ x ≠ 1và x ≠ - 2

Vậy điều kiện để biểu thức xác định là x ≠ 1 và x ≠ - 2.

b. Biểu thức 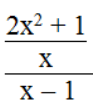xác định khi: x ≠ 0 và x – 1 ≠ 0 ⇔ x ≠ 0 và x ≠ 1

Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 1.

c. Biểu thức 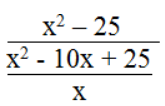xác định khi x²- 10x + 25 ≠ 0 và x ≠ 0

x² – 10x + 25 ≠ 0 ⇔ (x – 5)² ≠ 0 ⇔ x ≠ 5

Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 5

d. Biểu thức 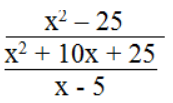xác định khi x² + 10x + 25 ≠ 0 và x - 5 ≠ 0

x² + 10x + 25 ≠ 0 ⇔ (x + 5)² ≠ 0 ⇔ x ≠ - 5

x – 5 ≠ 0 ⇔ x ≠ 5

Vậy điều kiện để biểu thức xác định là x ≠ 5 và x ≠ - 5.

Bài 63 trang 40 SBT Toán 8 Tập 1: Tìm giá trị của x để giá trị của các biểu thức trong bài tập 62 bằng 0.

Lời giải:

a. Biểu thức 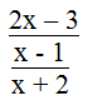xác định khi x ≠ 1 và x ≠ - 2

Ta có: 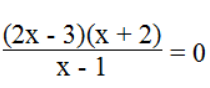khi (2x – 3)(x + 2) = 0 và x – 1 ≠ 0

(2x – 3)(x + 2) = 0 ⇔

x – 1 ≠ 0 ⇔ x ≠ 1

x = - 2 không thỏa mãn điều kiện

Vậy x = 1,5 thì biểu thức 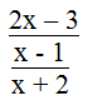có giá trị bằng 0.

b. Biểu thức 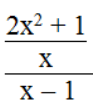xác định khi x ≠ 0 và x ≠ 1

Ta có: khi 2x² + 1 = 0 và x(x – 1) ≠ 0

Ta có: 2x² ≥ 0 nên 2x² + 1 ≠ 0 mọi x.

Không có giá trị nào của x để biểu thức 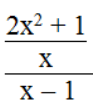có giá trị b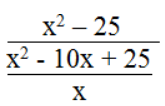ằng 0.

c. Biểu thức xác định khi x ≠ 0 và x ≠ 5.

Ta có: 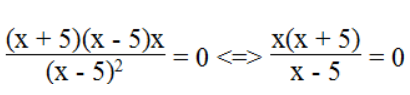khi x(x + 5) = 0 và x – 5 ≠ 0

x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5

x = 0 không thỏa mãn điều kiện.

Vậy x = - 5 thì biểu thức 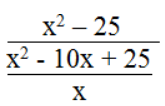có giá trị bằng 0.

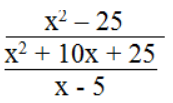
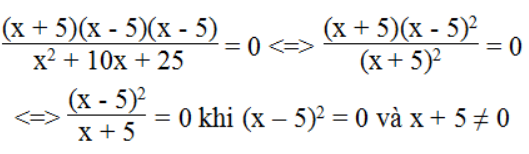
d. Biểu thức xác định khi x ≠ 5 và x ≠ - 5

(x – 5)² = 0 ⇔ x – 5 = 0 ⇔ x= 5

x = 5 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để biểu thức có giá trị bằng 0.