(SGK + SBT) Giải Toán 8 trang 41 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 41 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 41.
(SGK + SBT) Giải Toán 8 trang 41 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 41 Tập 1 (sách mới):
- Toán lớp 8 trang 41 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 41 (sách cũ)
Bài 64 trang 41 SBT Toán 8 Tập 1: Tìm điều kiện của x để giá trị của biểu thức được xác định và chứng minh rằng với điều kiện đó biểu thức không phụ thuộc vào biến x:
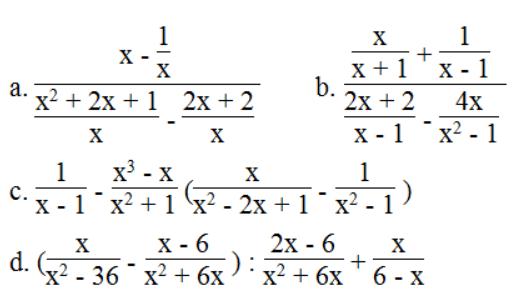
Lời giải:
a.
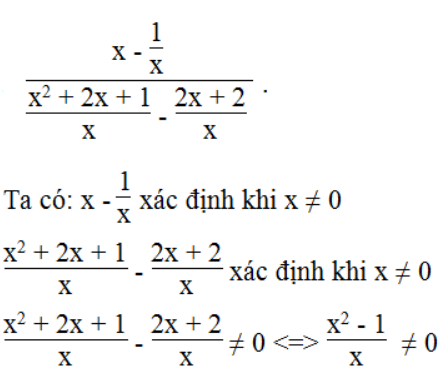
⇔ x2 – 1 ≠ 0
⇔ (x + 1)(x – 1) ≠ 0
⇔ x ≠ - 1 và x ≠ 1
Vậy với x ≠ 0, x ≠ 1 và x ≠ - 1 thì biểu thức xác định.
Ta có:
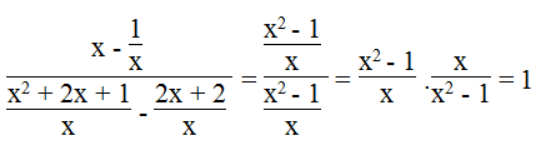
Vậy biểu thức không phụ thuộc vào biến x.
b.
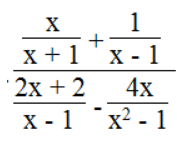
Ta có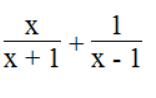 
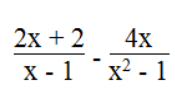
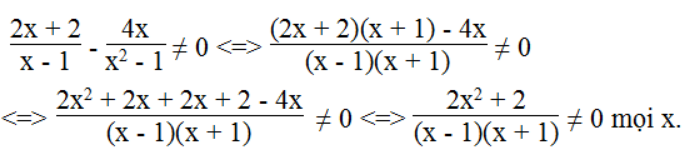
xác định khi x + 1 ≠ 0 và x – 1 ≠ 0 ⇒ x ≠ ± 1
xác định khi x – 1 ≠ 0 và x2 – 1 ≠ 0 ⇒ x ≠ ± 1
Vậy điều kiện để biểu thức xác định x ≠ ± 1
Ta có
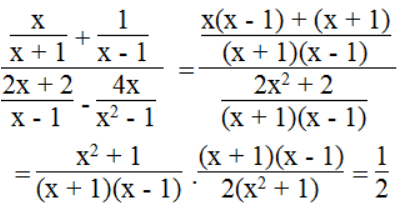
Vậy biểu thức không phụ thuộc vào biến x.
c.
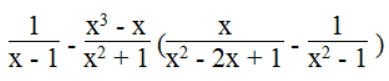
Biểu thức xác định khi x – 1 ≠ 0, x2 – 2x + 1 ≠ và x2 – 1 ≠ 0
x – 1 ≠ 0 ⇒ x ≠ 1
x2 – 2x + 1 ≠ 0 ⇒ (x – 1)2 ≠ 0 ⇒ x ≠ 1
x2 – 1 ≠ 0 ⇒ (x – 1)(x + 1) ≠ 0 ⇒ x ≠ -1 và x ≠ 1
Vậy biểu thức xác định với x ≠ -1 và x ≠ 1
Ta có:
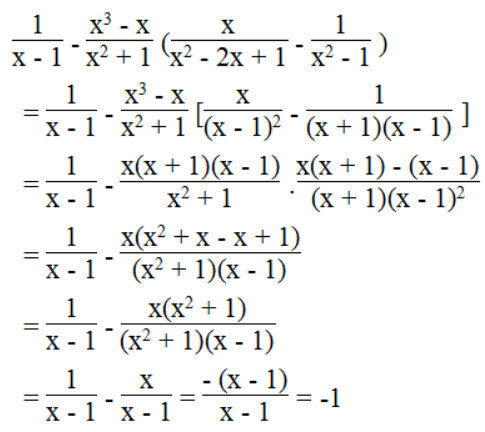
Vậy biểu thức không phụ thuộc vào biến x.
d.
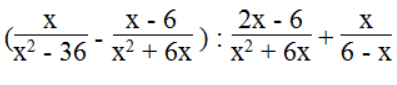
Biểu thức xác định khi x2 – 36 ≠ 0, x2 + 6x ≠ 0, 6 – x ≠ 0 và 2x – 6 ≠ 0
x2 – 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x2 + 6x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
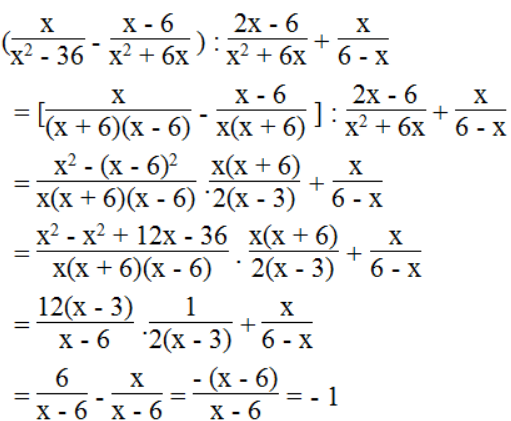
Vậy biểu thức không phụ thuộc vào biến x.
Bài 65 trang 41 SBT Toán 8 Tập 1: Chứng minh rằng:
a. Giá trị của biểu thức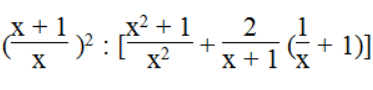 
bằng 1 với mọi giá trị x ≠ 0 và x ≠ 1.
b. Giá trị của biểu thức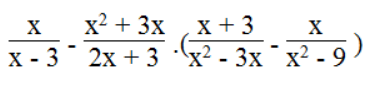 
bằng 1 khi x ≠ 0, x ≠ 3, x ≠ - 3 và x ≠ - 3/2 .
Lời giải:
a.
Biểu thức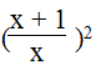 
xác định khi x ≠ 0
Biểu thức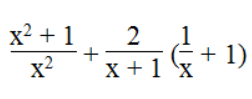 
xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
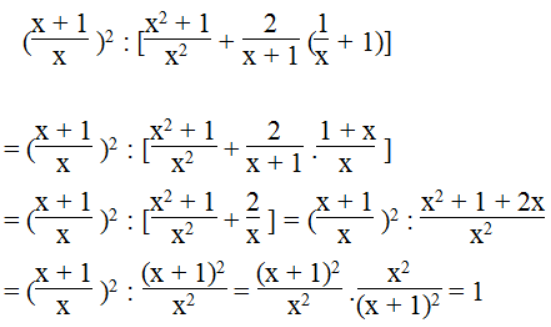
Vậy giá trị của biểu thức 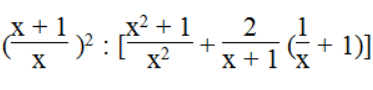bằng 1 với mọi giá trị x ≠ 0 và x ≠ 1.
b. Biểu thức 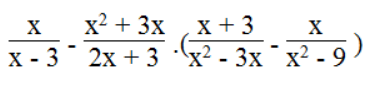xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x2 – 3x ≠ 0 và x2 – 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
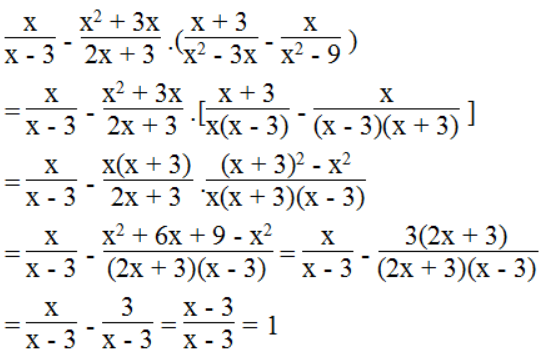
Vậy giá trị của biểu thức 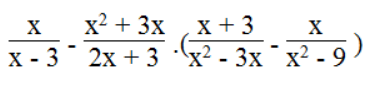bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3
Bài 66 trang 41 SBT Toán 8 Tập 1: Chú ý nếu c > 0 thì (a + b)2 + c và (a – b)2 + c đều dương với mọi a, b; áp dụng điều này chứng minh rằng:
a. Với mọi giá trị của x khác 1, biểu thức:
luôn luôn có giá trị dương.
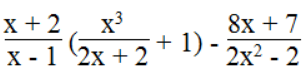
b. Với mọi giá trị của x khác 0 và khác – 3, biểu thức:
luôn luôn có giá trị âm.
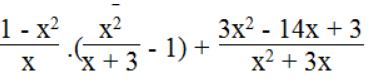
Lời giải:
a. Điều kiện x ≠ 1 và x ≠ - 1
Ta có:
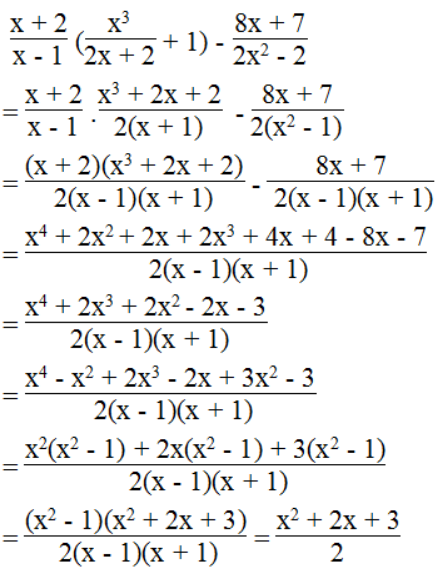
Biểu thức dương khi x2 + 2x + 3 > 0
Ta có: x2 + 2x + 3 = x2 + 2x + 1 + 2 = (x + 1)2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1
b. Điều kiện x ≠ 0 và x ≠ -3
Ta có:
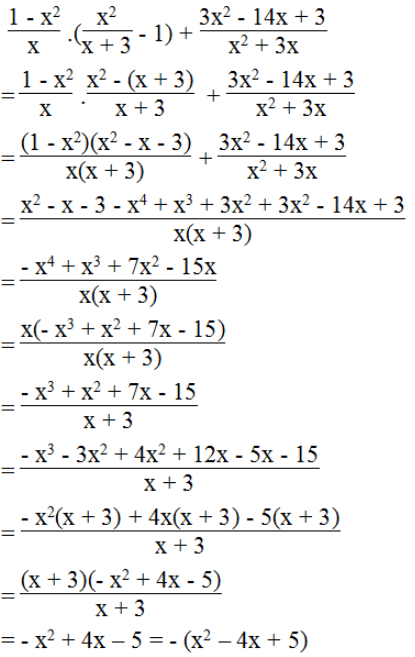
Vì x2 – 4x + 5 = x2 – 4x + 4 + 1 = (x – 2)2 + 1 > 0 với mọi giá trị của x nên
-[(x – 2)2 + 1] < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
