Giải Toán 8 trang 61 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 61 Tập 1 trong Bài 1: Định lí Pythagore Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 61.

Giải Toán 8 trang 61 Tập 1 Chân trời sáng tạo

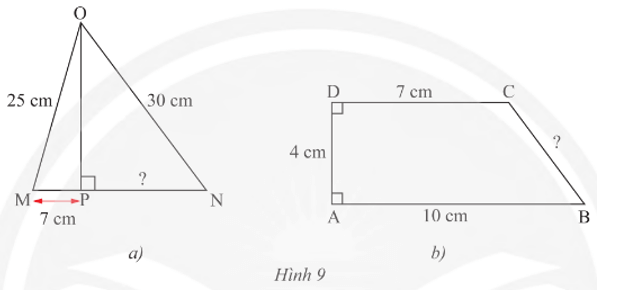
Thực hành 3 trang 61 Toán 8 Tập 1: Tính các độ dài PN và BC trong Hình 9.

Lời giải:

a) Áp dụng định lí Pythagore vào tam giác OPM vuông tại P, ta có:

OM² = OP² + MP²

Suy ra OP² = OM² – MP² = 25² – 7² = 625 – 49 = 576.

Áp dụng định lí Pythagore vào tam giác OPN vuông tại P, ta có:

ON² = OP² + PN²

Suy ra PN² = ON² – OP² = 30² – 576 = 900 – 576 = 324 = 18².

Vậy PN = 18 cm.

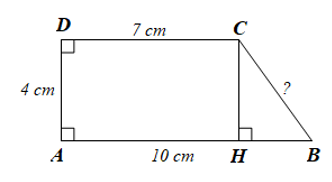
b)

Vẽ CH vuông góc với AB như hình vẽ, ta có:

CH = 4 cm; HB = 10 – 7 = 3 (cm).

Áp dụng định lí Pythagore vào tam giác CHB vuông tại H, ta có:

BC² = CH² + HB² = 4² + 3² = 25 = 5².

Vậy BC = 5 cm.

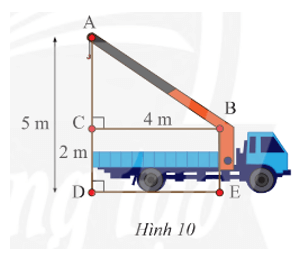
Vận dụng 3 trang 61 Toán 8 Tập 1: Tính chiều dài cần cẩu AB trong Hình 10.

Lời giải:

Xét tam giác ABC có CB = 4 m, AC = AD – CD = 5 – 2 = 3 (m).

Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:

AB² = AC² + CB² = 3² + 4² = 25 = 5².

Suy ra AB = 5 m.

Vậy chiều dài cần cẩu AB là 5 m.

Bài 1 trang 61 Toán 8 Tập 1: Cho tam giác ABC vuông tại A.

a) Tính độ dài cạnh BC nếu biết AB = 7 cm, AC = 24 cm.

b) Tính độ dài cạnh AB nếu biết AC = 2 cm, BC = $\sqrt{13}$ cm.

c) Tính độ dài cạnh AC nếu biết BC = 25 cm, AB = 15 cm.

Lời giải:

a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC² = AB² + AC² = 7² + 24² = 49 + 576 = 625 = 25².

Vậy BC = 25 cm.

b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC² = AB² + AC².

Suy ra AB² = BC² – AC² = ${\left(\sqrt{13}\right)}^2$ – 2² = 13 – 4 = 9 = 3².

Vậy AB = 3 cm.

c) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:

BC² = AB² + AC².

Suy ra: AC² = BC² – AB² = 25² – 15² = 625 – 225 = 400 = 20².

Vậy AC = 20 cm.

Lời giải bài tập Toán 8 Bài 1: Định lí Pythagore Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 58

• Giải Toán 8 trang 59

• Giải Toán 8 trang 60

• Giải Toán 8 trang 62