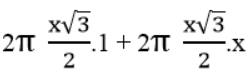Bài 16, 17, 18, 19 trang 167 SBT Toán 9 Tập 2

---

Bài 16, 17, 18, 19 trang 167 SBT Toán 9 Tập 2

Bài 16 trang 167 Sách bài tập Toán 9 Tập 2: Một chiếc cốc dạng hình nón chứa đầy rượu (hình sau). Cụ Bá uống một lượng rượu nên “chiều cao” của rượu còn lại trong cốc bằng một nửa chiều cao ban đầu . Hỏi cụ Bá đã uống bao nhiêu phần rượu trong cốc?

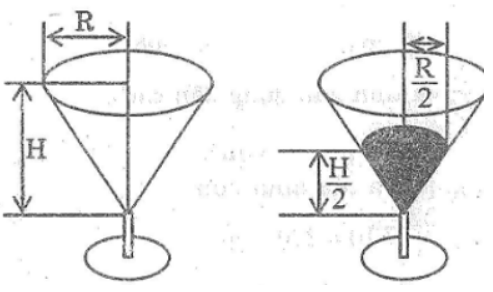
Lời giải:

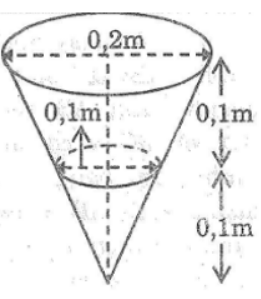
Bài 17 trang 167 Sách bài tập Toán 9 Tập 2: Người ta minh họa một cái xô đựng nước như hình dưới .Thể tích nước chứa đầy xô sẽ là (tính theo cm³):

Lời giải:

Thể tích hình nón có đường kính đáy 0,2m:

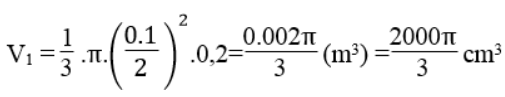
Thể tích hình nón có đường kính đáy 0,1m:

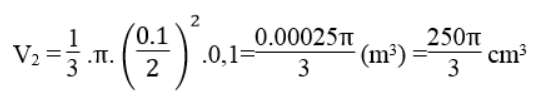
Thể tích nước chứa đầy xô là :

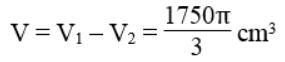
Vậy chọn đáp án B

Bài 18 trang 167 Sách bài tập Toán 9 Tập 2: Diện tích toàn phần của hình nón theo các kích thước của hình bên dưới là:

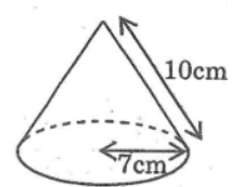
A.220    B.264     C.308     D.374

(Chọn π =22/7 và tính gần đúng đến cm³)

Lời giải:

Diện tích xung quanh của hình nón :

S_xq = π.r.l = (22/7).7.10 =220 (cm²)

Diện tích đáy của hình nón:

S_đáy = π.r² = (22/7).72= 154 (cm²)

Diện tích toàn phần của hình nón :

S_TP = S_xq + S_đáy = 220 + 154 =374 (cm²)

Vậy chọn đáp án D

Bài 19 trang 167 Sách bài tập Toán 9 Tập 2: Cho hình bình hành ABCD với AB=1,AD=x (x > 0) và góc (BAD) = 60°

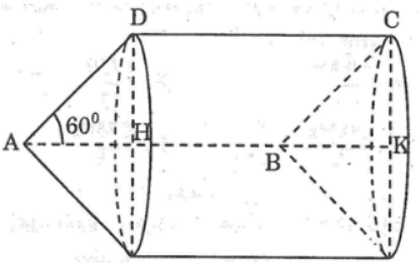
a.Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S₁ của hình tạo thành khi quay cạnh AD

b.Xác định giá trị x khi S = S₁ và S = 2S₁

Lời giải:

a.*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón

Trong tam giác AHD,ta có:

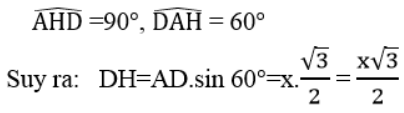
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ

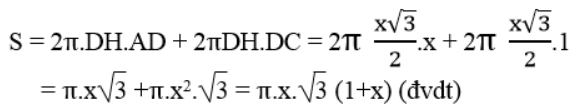
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = 1, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón

Ta có:

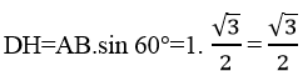
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ

S₁ = 2πDH.AB + 2πDH.AD =

= π.√3 +π.x.√3 = π.√3 (x+1) (đvdt)

b.*Ta có: S = S1 ⇔ π.x.√3 (1+x) = π.√3 (x+1)

⇔ x(1+x) = x +1 ⇔ x² -1 =0 ⇔ (x+1)(x-1) = 0

Vì x > 0 nên x+1 > 0

suy ra: x-1 = 0 ⇔ x = 1

*Ta có: S = 2S₁ ⇔ .x.√3 (1+x) = 2.π.√3 (x+1)

⇔ x(x+1) = 2(x+1) ⇔ x² – x -2 =0

⇔ x² – 2x +x - 2 = 0 ⇔ (x+1)(x-2) = 0

Vì x > 0 nên x+1 > 0

suy ra : x-2 = 0 ⇔ x = 2