Bài 16, 17, 18, 19 trang 52 SBT Toán 9 Tập 2

---

Bài 16, 17, 18, 19 trang 52 SBT Toán 9 Tập 2

Bài 16 trang 52 Sách bài tập Toán 9 Tập 2: Giải các phương trình:

a. 5x² – 20 = 0     b. -3x² + 15 = 0

c. 1,2x² – 0,192 = 0     d. 1172,5x² + 42,18 = 0

Lời giải:

a.Ta có: 5x² – 20 = 0 ⇔ 5x²= 20 ⇔ x² = 4 ⇔ x = ±2

Vậy phương trình có hai nghiệm x₁ = 2, x₂ = -2

b.Ta có: -3x² + 15 = 0 ⇔ -3x² = -15 ⇔ x² = 5 ⇔ x = ±√5

Vậy phương trình có hai nghiệm x₁ = √5 , x₂ = -√5

c.Ta có: 1,2x² – 0,192 = 0 ⇔ 1,2x² = 0,192 ⇔ x² = 0,16 ⇔ x = ±0,4

Vậy phương trình có hai nghiệm x₁= 0,4, x₂ = -0,4

d.Ta có: x² ≥ 0 ⇒ 1172,5x² ≥ 0 ⇒ 1172,5x² + 42,18 > 0

Vậy không có giá trị nào của x thỏa mãn phương trình nên phương trình vô nghiệm.

Bài 17 trang 52 Sách bài tập Toán 9 Tập 2: Giải các phương trình :

a. (x – 3)² = 4    b. (1/2 - x)²– 3 = 0

c. (2x - 2 )² – 8 = 0     d. (2,1x – 1,2)²– 0,25 = 0

Lời giải:

a.Ta có : (x – 3)² = 4 ⇔ (x – 3)² – 22 = 0

⇔ [(x – 3) + 2][(x – 3) – 2] = 0 ⇔ (x – 1)(x – 5) = 0

⇔ x – 1 = 0 hoặc x – 5 = 0 ⇔ x = 1 hoặc x = 5

Vậy phương trình có hai nghiệm x₁ = 1, x₂ = 5

b.Ta có: (1/2 - x)² – 3 = 0 ⇔ (1/2 - x)² – (√3 )² = 0

⇔ [(1/2 - x) + √3 ][(1/2 - x) - √3 ] = 0

⇔ (1/2 + √3 – x)( 1/2 - √3 – x) = 0

⇔ 1/2 + √3 – x = 0 hoặc 1/2 - √3 – x = 0

⇔ x = 1/2 + √3 hoặc x = 1/2 - √3

Vậy phương trình có hai nghiệm x₁ = 1/2 + √3 , x₂ = 1/2 - √3

c.Ta có: (2x - √2 )² – 8 = 0 ⇔ (2x - √2 )² – (2√2 )² = 0

⇔ [(2x - √2 ) + 2√2 ][(2x - √2 ) - 2√2 ] = 0

⇔ (2x - √2 + 2√2 )(2x - √2 - 2√2 ) = 0

⇔ (2x + √2 )(2x - 3√2 ) = 0

⇔ 2x + √2 = 0 hoặc 2x - 3√2 = 0

⇔ x = -√2/2 hoặc x = 3√2/2

Vậy phương trình có hai nghiệm x₁ = -√2/2 hoặc x₂ = 3√2/2

d.Ta có: (2,1x – 1,2)² – 0,25 = 0 ⇔ (2,1x – 1,2)² – (0,5)² = 0

⇔ [(2,1x – 1,2) + 0,5][(2,1x – 1,2) – 0,5] = 0

⇔ (2,1x – 1,2 + 0,5)(2,1x -1,2 – 0,5) = 0

⇔ (2,1x – 0,7)(2,1x – 1,7) = 0

⇔ 2,1x – 0,7 = 0 hoặc 2,1x – 1,7 = 0

⇔ x = (0,7)/(2,1) hoặc x = (1,7)/(2,1) ⇔ x = 1/3 hoặc x = 17/21

Vậy phương trình có hai nghiệm x₁ = 1/3 hoặc x₂ = 17/21

Bài 18 trang 52 Sách bài tập Toán 9 Tập 2: Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số.

a. x² – 6x + 5 = 0    b. x² – 3x – 7 = 0

c. 3x² – 12x + 1 = 0     d. 3x² – 6x + 5 = 0

Lời giải:

a. Ta có : x² – 6x + 5 = 0 ⇔ x² – 2.3x + 5 + 4 = 4

⇔ x² – 2.3x + 9 = 4 ⇔ (x – 3)² = 2²

⇔ x – 3 = ±2 ⇔ x – 3 = 2 hoặc x – 3 = -2

⇔ x = 1 hoặc x = 5

Vậy phương trình có hai nghiệm x₁ = 1, x₂ = 5

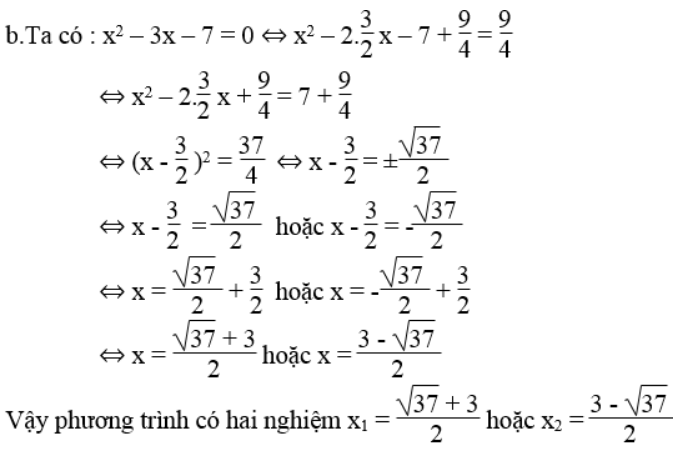
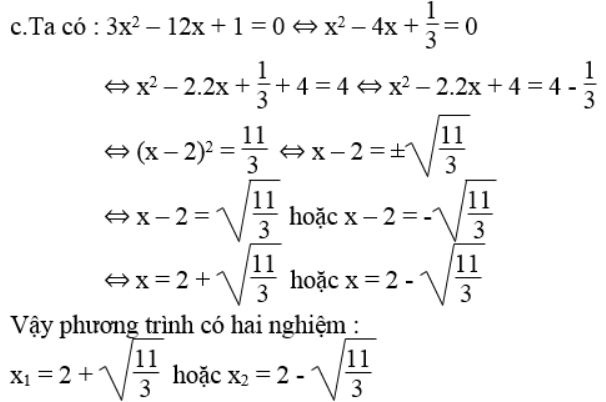
d.Ta có : 3x² – 6x + 5 = 0 ⇔ x²- 2x + 5/3 = 0

⇔ x² – 2x + 5/3 + 1 = 1 ⇔ x² – 2x + 1 = 1 - 5/3

⇔ (x – 1)² = -2/3

Ta thấy (x – 1)² ≥ 0 và -2/3 < 0

Vậy phương trình vô nghiệm.

Bài 19 trang 52 Sách bài tập Toán 9 Tập 2: Nhận thấy rằng phương trình tích (x + 2)(x – 3) = 0, hay phương trình bậc hai x² – x – 6 = 0, có hai nghiệm là x₁ = -2, x₂ = 3. Tương tự, hãy lập những phương trình bậc hai mà nghiệm mỗi phương trình là một trong những cặp số sau :

a. x₁ = 2, x₂ = 5     b. x₁ = -1/2 , x₂ = 3

c. x₁ = 0,1, x₂ = 0,2     d. x₁ = 1 - √2 , x₂ = 1 + √2

Lời giải:

a. Hai số 2 và 5 là nghiệm của phương trình :

(x – 2)(x – 5) = 0 ⇔ x² – 7x + 10 = 0

b. Hai số -1/2 và 3 là nghiệm của phương trình :

(x + 1/2 )(x – 3) = 0 ⇔ 2x² – 5x – 3 = 0

c. Hai số 0,1 và 0,2 là nghiệm của phương trình :

(x – 0,1)(x – 0,2) = 0 ⇔ x² – 0,3x + 0,02 = 0

d. Hai số 1 - √2 và 1 + √2 là nghiệm của phương trình :

[x – (1 - √2 )][x – (1 + √2 )] = 0

⇔ x² – (1 + √2 )x – (1 - √2 )x + (1 - √2 )(1 + √2 ) = 0

⇔ x² – 2x – 1 = 0