Bài 5.2, 5.3, 5.4 trang 69 SBT Toán 9 Tập 1

---

Bài 5.2, 5.3, 5.4 trang 69 SBT Toán 9 Tập 1

Bài 2 trang 69 Sách bài tập Toán 9 Tập 1: a) Hệ số góc của đường thẳng đi qua gốc tọa độ và điểm M(√3, √3/2)

A. √3;     B. √3/2;     C. 1/2;     D. 3/2.

b) Hệ số góc của đường thẳng đi qua hai điểm P(1; √3 + √2) và Q(√3; 3 + √2) là:

A. -√3;    B. (√3 – 1);    C. (1 - √3);    D. √3.

Lời giải:

a) Chọn C.     b) Chọn D.

Bài 3 trang 69 Sách bài tập Toán 9 Tập 1: a) Góc hợp bởi đường thẳng 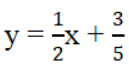và trục Ox là:

A. 26^o34’;     B. 30^o;     C. 60^o;     D. 30^o58’.

b) Góc hợp bởi đường thẳng 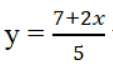và trục Ox là:

A. 54^o28’;     B. 81^o52’;     C. 21^o48’;     D. 63^o26’.

(Chú ý: Dùng máy tính bỏ túi tính góc chính xác đến phút).

Lời giải:

a) Chọn A. b) Chọn C.

Bài 4 trang 69 Sách bài tập Toán 9 Tập 1: Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:

A(4;5)     B(1;-1)    C(4;-4)    D(7; -1).

a) Viết phương trình của các đường thẳng AB, BC, CD và DA.

b) Tính (theo độ, phút) các góc của tứ giác ABCD bằng máy tính bỏ túi.

Lời giải:

a) Phương trình của đường thẳng AB có dạng: y = ax + b.

Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:

5 = a.4 + b (1)

-1 = a.1 + b (2)

Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.

Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.

Vậy phương trình đường thẳng AB là: y = 2x – 3.

Làm tương tự như trên, ta có:

Phương trình đường thẳng BC là: y = -x.

Phương trình đường thẳng CD là: y = x – 8.

Phương trình đường thẳng DA là: y = -2x + 13.

b) (h.bs.3) Hai đường chéo AC và BD vuông góc với nhau tại I.

- Đường thẳng AB có hệ số góc bằng 2, do đó ta có

tgα = 2 ⇒ α = 63^o26’ (tính trên máy tính bỏ túi).

Suy ra ∠(ABD) ≈ 63^o26’.

Tam giác ABD cân, nên cũng có ∠(ADB) ≈ 63^o26’.

Từ đó suy ra ∠(BAD) = 180^o - 2. 63^o26’ ≈ 53^o8’.

Đường thẳng BC có hệ số góc bằng -1 nên BC là phân giác của góc vuông phần tư thứ tư của mặt phẳng tọa độ Oxy.

Đường thẳng CD có hệ số góc bằng 1, do đó CD song song với đường thẳng phân giác của góc phần tư thứ nhất.

Từ đó suy ra: ∠(BCD) = 180^o - 45^o - 45^o = 90^o.

Và do đó: ∠(ABC) = ∠(ADC) = (360^o - ∠(BCD) - ∠(BAD) ): 2 ≈ 108^o26’.