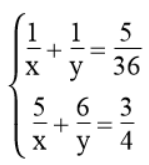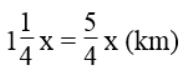Bài 42, 43, 44, 45, 46, 47, 48, 49 trang 14 SBT Toán 9 Tập 2
Bài 42, 43, 44, 45, 46, 47, 48, 49 trang 14 SBT Toán 9 Tập 2
Bài 42 trang 14 Sách bài tập Toán 9 Tập 2: Trong phòng học có một ghế dài. Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ. Nếu xếp mỗi ghế 4 học sinh thì thừa một ghế. Hỏi có bao nhiêu ghế và bao nhiêu học sinh?
Lời giải:
Gọi số ghế trong phòng học là x (ghế), số học sinh của lớp là y (học sinh). Điều kiện x, y ∈N*
Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ, ta có phương trình: 3x + 6 = y
Nếu xếp mỗi ghế 4 học sinh thì thừa một ghế, ta có phương trình: (x – 1)4=y
Ta có hệ phương trình:
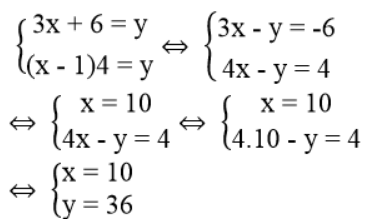
Giá trị của x và y thỏa điều kiện bài toán.
Vậy trong phòng học có 10 ghế và 36 học sinh.
Bài 43 trang 14 Sách bài tập Toán 9 Tập 2: Trên một cánh đồng cấy 60ha lúa giống mới và 40ha lúa giống cũ. Thu hoạch được tất cả 460 tấn thóc. Hỏi năng suất mỗi loại lúa trên 1ha là bao nhiêu biết rằng 3ha trồng lúa mới thu hoạch được ít hơn 4ha trồng lúa cũ là 1 tấn.
Lời giải:
Gọi x, y (tấn) lần lượt là năng suất của giống lúa mới và giống lúa cũ trên 1ha. Điều kiện: x > 0, y > 0.
Vì 60ha lúa giống mới và 40ha lúa giống cũ thu hoạch được tất cả 460 tấn thóc ta có: 60x + 40y = 460
Vì 3ha trồng lúa mới thu hoạch được ít hơn 4ha trồng lúa cũ là 1 tấn nên ta có: 4y – 3x = 1
Ta có hệ phương trình:
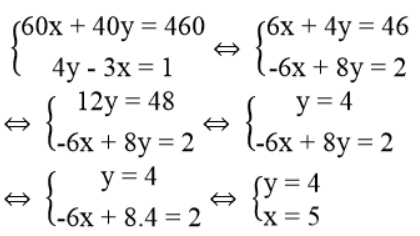
Giá trị của x và y thỏa điều kiện bài toán.
Vậy năng suất lúa giống mới là 5 tấn/ha,
năng suất lúa giống cũ là 4 tấn/ha.
Bài 44 trang 14 Sách bài tập Toán 9 Tập 2: Hai người thợ cùng xây một bức tường trong 7 giờ 12 phút thì xong (vôi, vữa và gạch có công nhân khác vận chuyển). Nếu người thứ nhất làm xong trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai xây được 3/4 bức tường. Hỏi mỗi người làm một mình thì bao lâu mới xây xong bức tường?
Lời giải:
Gọi x, y (giờ) lần lượt là thời gian mà người thứ nhất và người thứ hai một mình xây xong bức tường.
Điều kiện: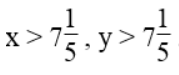 
Như vậy, trong 1 giờ người thứ nhất xây được 1/x (bức tường), người thứ hai xây được 1/y (bức tường).
Trong 1 giờ, cả hai người xây được 1: 36/5 = 5/36 (bức tường)
Ta có phương trình: 1/x + 1/y = 5/36
Nếu người thứ nhất làm trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai xây được 3/4 bức tường, ta có phương trình: 5/x + 6/y = 3/4
Ta có hệ phương trình: 
Đặt m = 1/x , n = 1/y , ta có:
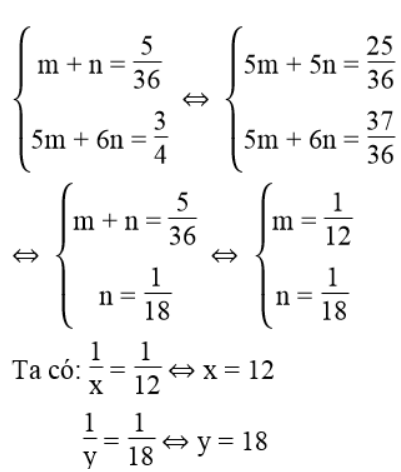
Giá trị của x và y thỏa điều kiện bài toán.
Vậy người thứ nhất làm một mình xong bức tường trong 12 giờ, người thứ hai làm một mình xong bức tường trong 18 giờ.
Bài 45 trang 14 Sách bài tập Toán 9 Tập 2: Hai công nhân cùng sơn cửa cho một công trình trong 4 ngày thì xong việc. Nếu người thứ nhất làm một mình trong 9 ngày rồi người thứ hai đến cùng làm tiếp trong 1 ngày nữa thì xong việc. Hỏi mỗi người làm một mình bao lâu thì xong việc?
Lời giải:
Gọi x, y (ngày) lần lượt là thời gian mà người thứ nhất và người thứ hai làm riêng xong công việc. Điều kiện: x > 4, y > 4.
Như vậy, trong 1 ngày người thứ nhất làm được 1/x (công việc), người thứ hai làm được 1/y (công việc).
Trong 1 ngày, cả hai người làm được 1 : 4 = 1/4 (công việc)
Ta có phương trình: 1/x + 1/y = 14
Nếu người thứ nhất làm một mình trong 9 ngày rồi người thứ hai đến cùng làm tiếp trong 1 ngày nữa thì xong việc, ta có phương trình:
10/x + 1/y = 1
Ta có hệ phương trình:
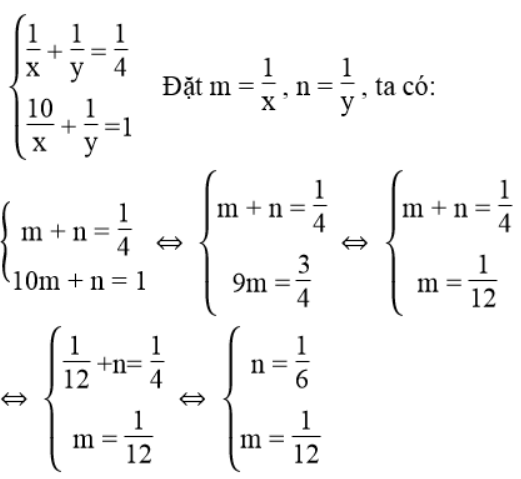
Ta có: 1/x = 1/12 ⇔ x = 12
1/y = 1/6 ⇔ y = 6
Giá trị của x và y thỏa điều kiện bài toán.
Vậy người thứ nhất làm một mình xong công việc trong 12 ngày, người thứ hai làm một mình xong công việc trong 6 ngày.
Bài 46 trang 14 Sách bài tập Toán 9 Tập 2: Hai cần cẩu lớn bốc dỡ một lô hàng ở cảng Sài Gòn. Sau 6 giờ có thêm năm cần cẩu bé (công suất bé hơn) cùng làm việc. Cả bảy cần cẩu làm việc 3 giờ nữa thì xong. Hỏi mỗi cần cẩu làm việc một mình bao lâu thì xong việc, biết rằng nếu cả bảy cần cẩu làm việc một mình bao lâu thì xong việc, biết rằng nếu cả bảy cần cẩu cùng làm việc từ đầu thì trong 4 giờ làm việc.
Lời giải:
Gọi x, y (giờ) lần lượt là thời gian mà một cần cẩu lớn và một cần cẩu nhỏ làm xong công việc. Điều kiện: y > x > 12
Như vậy, trong 1 giờ cần cẩu lớn làm được 1/x (công việc), cần cẩu nhỏ làm được 1/y (công việc).
Trong 1 giờ, hai cần cẩu lớn và năm cần cẩu nhỏ làm được 1 : 4 = 1/4 (công việc)
Ta có phương trình: 2/x + 5/y = 1/4
Hai cần cẩu lớn làm trong 6 giờ và năm cần cẩu nhỏ làm trong 3 giờ nữa thì xong việc, ta có phương trình:
12/x + 15/y = 1
Ta có hệ phương trình:
Ta có: 1x = 1/24 ⇔ x = 24
1y = 1/30 ⇔ y = 30
Giá trị của x và y thỏa điều kiện bài toán.
Vậy một cần cẩu loại lớn làm xong công việc trong 24 giờ, một cần cẩu loại nhỏ làm xong công việc trong 30 giờ.
Bài 47 trang 14 Sách bài tập Toán 9 Tập 2: Bác Toàn đi xe đạp từ thị xã về làng, cô ba Ngần cũng đi xe đạp, nhưng từ làng lên thị xã. Họ gặp nhau khi bác Toàn đã đi được 1 giờ rưỡi, còn cô ba Ngần đã đi được 2 giờ. Một lần khác hai người cũng đi từ hai địa điểm như thế nhưng họ khởi hành đồng thời. Sau 1 giờ 15 phút họ còn cách nhau 10,5km. Tính vận tốc của mỗi người, biết rằng làng cách thị xã 38km.
Lời giải:
Gọi x, y (km/h) lần lượt là vận tốc của bác Toàn và cô ba Ngần đi. Điều kiện: x > 0, y > 0.
Vì hai người đi ngược chiều nhau, bác Toàn đi 1 giờ 30 phút, cô ba Ngần đi 2 giờ thì gặp nhau nên ta có phương trình: 1,5x + 2y = 38
Quãng đường bác Toàn đi trong 1 giờ 15 phút là: 
Quãng đường cô ba Ngần đi trong 1 giờ 15 phút là: 
Sau 1 giờ 15 phút, hai người còn cách nhau 10,5km nên ta có phương trình:
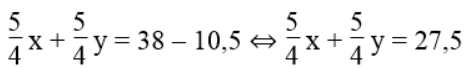
⇔ 5x + 5y = 110
Ta có hệ phương trình:
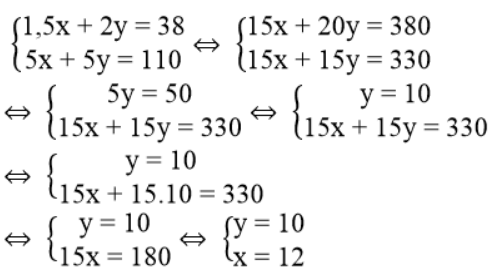
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của bác Toàn là 12km/h, vận tốc của cô ba Ngần là 10km/h.
Bài 48 trang 14 Sách bài tập Toán 9 Tập 2: Ga Sài Gòn cách ga Dầu Giây 65km. Xe khách ở thành phó Hồ Chí Minh, xe hàng ở Dầu Giây đi ngược chiều nhau và xe khách khởi hành sau xe hàng 36 phút, sau khi xe khách khởi hành đồng thời cùng đi Hà Nội thì sau 13 giờ hai xe gặp nhau. Tính vận tốc của mỗi xe, biết rằng xe khách đi nhanh hơn xe hàng.
Lời giải:
Gọi x, y (km/h) lần lượt là vận tốc của xe khách và xe hàng. Điều kiện: x > y > 0.
Sau khi xe khách đi được 24 phút = 2/5 giờ thì xe hàng đi được:
24 + 36 = 60 (phút) = 1 (giờ)
Hai xe đi ngược chiều nhau nên ta có phương trình:
(2/5)x + y = 65 ⇔ 2x + 5y = 325
Hai xe khởi hành đồng thời cùng đi Hà Nội thì sau 13 giờ hai xe gặp nhau, ta có phương trình: 13x – 13y = 65 ⇔ x – y = 5
Ta có hệ phương trình:
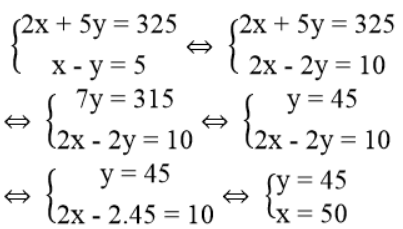
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của xe khách là 50km/h, vận tốc của xe hàng là 45km/h.
Bài 49 trang 14 Sách bài tập Toán 9 Tập 2: Để sửa một ngôi nhà cần một số thợ làm việc trong một thời gian quy định. Nếu giảm 3 người thì thời gian kéo dài 6 ngày. Nếu tăng thêm 2 người thì xong sớm 2 ngày. Hỏi theo quy định cần bao nhiêu thợ và làm trong bao nhiêu ngày, biết rằng khả năng lao động của mỗi thợ đều như nhau?
Lời giải:
Gọi x (người) là số thợ cần thiết để sửa xong ngôi nhà, y (ngày) là thời gian dự định để làm xong. Điều kiện: x ∈N*, y > 0.
Số ngày công để hoàn thành công việc là xy (ngày).
Nếu giảm 3 người thì thời gian kéo dài 6 ngày, ta có phương trình:
(x – 3)(y + 6) = xy ⇔ xy + 6x – 3y – 18 = xy ⇔ 2x – y = 6
Nếu tăng thêm 2 người thì xong sớm 2 ngày, ta có phương trình:
(x + 2)(y – 2) = xy ⇔ xy – 2x + 2y – 4 = xy ⇔ -x + y = 2
Ta có hệ phương trình:
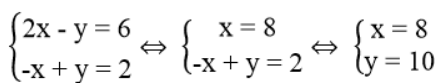
Giá trị của x và y thỏa điều kiện bài toán.
Vậy cần 8 người thợ làm việc trong 10 ngày thì xong ngôi nhà.
