Bài 50 trang 15 SBT Toán 9 Tập 2

---

Bài 50 trang 15 SBT Toán 9 Tập 2

Bài 50 trang 15 Sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD cạnh y (cm). Điểm E thuộc cạnh AB. Điểm G thuộc tia AD sao cho AG = AD + (3/2)EB. Dựng hình chữ nhật GAEF. Đặt EB = 2x (cm).

Tính x và y để diện tích hình chữ nhật bằng diện tích hình vuông và ngũ giác ABCFG có chu vi bằng 100 + 4√(13) (cm).

Lời giải:

Vì E thuộc cạnh AB nên EB < AB hay 2x < y

Ta có: AE = AB – EB = y – 2x (cm)

AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)

Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:

(y – 2x)(y + 3x) = y²

Theo định lí Pitago, ta có: FC² = EB² + DG²

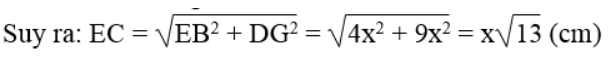
Chu vi ngũ giác ABCFG:

PABCFG = AB + BC + CF + FG + GA

= AB + BC + CF + FG + GD + DA

= y + y + x√(13) + y – 2x + 3y + y = x(1 + √(13) ) + 4y

Vì chu vi ngũ giác ABCFG bằng 100 + 4√(13) (cm) nên ta có phương trình:

x(1 + √(13) ) + 4y = 100 + 4√(13)

Ta có hệ phương trình:

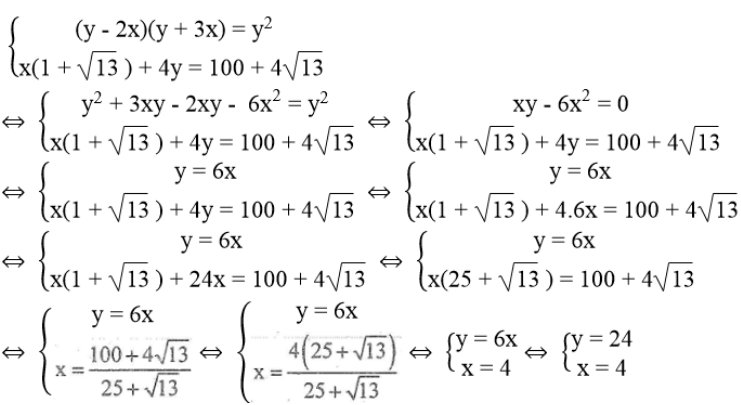
Giá trị của x và y thỏa điều kiện bài toán.

Vậy x = 4 (cm), y = 24 (cm).