Bài 52, 53, 54, 55, 56, 57, 58, 59 trang 165 SBT Toán 9 Tập 1

---

Bài 52, 53, 54, 55, 56, 57, 58, 59 trang 165 SBT Toán 9 Tập 1

Bài 52 trang 165 Sách bài tập Toán 9 Tập 1: Cho đường tròn (I) nội tiếp tam giác ABC. Các tiếp điểm trên AC, AB theo thứ tự là D, E. Cho BC = a, AC = b, AB = c. Tính độ dài các đoạn tiếp tuyến AD, AE theo a, b, c.

Lời giải:

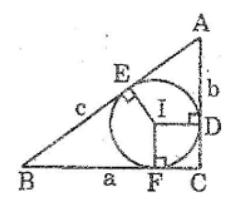
Gọi F là tiếp điểm của đường tròn (I) với BC.

Theo tính chất của hai tiếp tuyến cắt nhau, ta có:

AE = AD

BE = BF

CD = CF

Mà: AE = AB – BE

AD = AC – CD

Nên: AE + AD = (AB – BE) + (AC – CD) = AB + AC – (BE + CD)

= AB + AC – (BF + CF) = AB + AC – BC

Suy ra: AE + AD = c + b – a

Hay: AE = AD = (c + b - a)/2

Bài 53 trang 165 Sách bài tập Toán 9 Tập 1: Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I, r)

Lời giải:

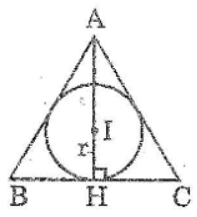
Gọi H là tiếp điểm của đường tròn (I) với BC.

Ta có: IH ⊥ BC (tính chất tiếp tuyến)

Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI là tia phân giác của góc BAC

Tam giác ABC đều nên AI cũng là đường cao của tam giác ABC. Khi đó A, I, H thẳng hàng

Ta có: HB = HC (tính chất tam giác đều)

Tam giác ABC đều nên I cũng là trọng tâm của tam giác ABC

Suy ra: AH = 3.HI = 3.r

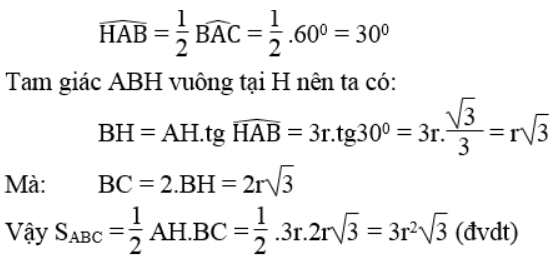
Bài 54 trang 165 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 3cm) và điểm A có OA = 5cm. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC)

a. Tính độ dài OH

b. Qua điểm M bất kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE

Lời giải:

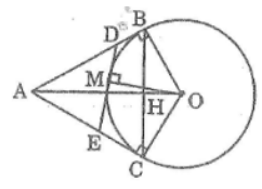
a. Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau). Suy ra ∆ABC cân tại A.

AO là tia phân giác của góc BAC (tính chất hai tiếp tuyến cắt nhau)

Suy ra AO là đường cao của tam giác ABC (tính chất tam giác cân)

Ta có: AO vuông góc với BC tại H

Lại có: AB ⊥ OB (tính chất tiếp tuyến)

Tam giác ABO vuông tại B có BH ⊥ AO

Theo hệ thức lượng trong tam giác vuông, ta có:

OB² = OH.OA ⇒ OH = OB²/OA = 32/5 = 1,8 (cm)

b. Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:

AO² = AB² + BO²

Suy ra: AB² = AO² – BO² = 5² – 3² = 16

AB = 4 (cm)

Theo tính chất của hai tiếp tuyến cắt nhau ta có:

DB = DM

EM = EC

Chu vi của tam giác ADE bằng:

AD + DE + EA = AD + DB + AE + EC

= AB + AC = 2AB = 2.4 = 8 (cm)

Bài 55 trang 165 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn vuông góc với nhau tại A (B và C là các tiếp điểm)

a. Tứ giác ABOC là hình gì? Vì sao?

b. Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.

c. Tính số đo góc DOE

Lời giải:

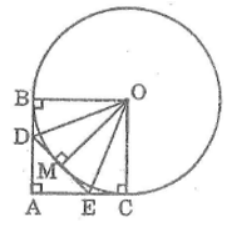
a. Ta có :

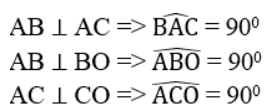
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật

Mặt khác : AB = AC (tính chất hai tiếp tuyến cắt nhau)

Suy ra tứ giác ABOC là hình vuông

b. Theo tính chất của hai tiếp tuyến cắt nhau ta có :

DB = DM

EM = EC

Chu vi của tam giác ADE bằng :

AD + DE + EA = AD + DM + ME + EA

= AD + DB + AE + EC = AB + AC = 2AB

Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:

AB = OB = 2 (cm)

Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)

c. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

OD là tia phân giác của góc BOM

Bài 56 trang 165 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A;AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).

Chứng minh rằng:

a. Ba điểm D, A, E thẳng hàng

b. DE tiếp xúc với đường tròn các đường kính BC

Lời giải:

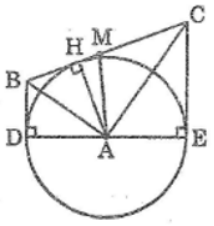
a. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

AB là tia phân giác của góc HAD

Vậy ba điểm D, A, E thẳng hàng.

b. Gọi M là trung điểm của BC

Theo tính chất của tiếp tuyến, ta có:

AD ⊥ DB; AE ⊥ CE

Suy ra: BD // CE

Vậy tứ giác BDEC là hình thang

Khi đó MA là đường trung bình của hình thang BDEC

Suy ra: MA // BD ⇒ MA ⊥ DE

Trong tam giác vuông ABC ta có : MA = MB = MC

Suy ra M là tâm đường tròn đường kính BC với MA là bán kính

Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC.

Bài 57 trang 165 Sách bài tập Toán 9 Tập 1: Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức : S = p.r

Lời giải:

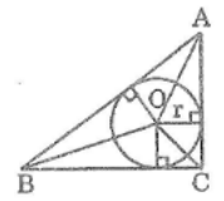
Gọi O là tâm đường tròn nội tiếp tam giác ABC

Nối OA, OB, OC

Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBC

Ta có : S_ABC = S_OAB + S_OAC + S_OBC

= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r

= (1/2)(AB + AC + BC).r

Mà AB + AC + BC = 2p

Nên S_ABC =(1/2).2p.r = p.r

Bài 58 trang 165 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E.

a. Tứ giác ADOE là hình gì? Vì sao ?

b. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.

Lời giải:

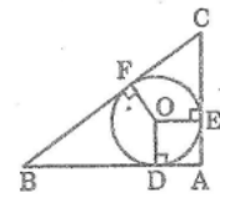
a. Ta có:

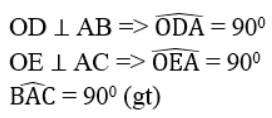
Tứ giác ADOE có ba góc vuông nên nó là hình chữ nhật

Lại có : AD = AE (tính chất hai tiếp tuyến giao nhau)

Vậy tứ giác ADOE là hình vuông

b. Áp dụng định lí Pitago vào tam giác vuông ABC ta có :

BC² = AB² + AC² = 3² + 4² = 25

Suy ra : BC = 5 (cm)

Theo tính chất hai tiếp tuyến giao nhau ta có:

AD = AE

BD = BF

CE = CF

Mà: AD = AB – BD

AE = AC – CF

Suy ra: AD + AE = AB – BD + (AC – CF)

= AB + AC – (BD + CF)

= AB + AC – (BF + CF)

= AB + AC – BC

Suy ra:

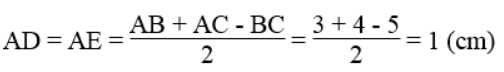
Bài 59 trang 165 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp. r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng: AB + AC = 2(R + r)

Lời giải:

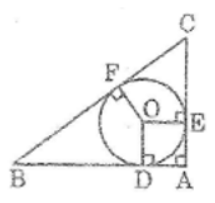
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.

Ta có: BC = 2R

Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F

Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.

Suy ra: AD = AE = EO = OD = r

Theo tính chất hai tiếp tuyến cắt nhau ta có:

AD = AE

BD = BF

CE = CF

Ta có: 2R + 2r = BF + FC + AD + AE

= (BD + AD) + (AE + CE)

= AB + AC

Vậy AB = AC = 2(R + r)