Chứng minh rằng một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng

Bài 1: Mặt cầu, Khối cầu

Haylamdo biên soạn và sưu tầm lời giải Bài 10 trang 46 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 10 (trang 46 sgk Hình Học 12 nâng cao):

a) Chứng minh rằng một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng và đáy là đa giác nội tiếp đường tròn.

b) Trong các hình hộp nội tiếp mặt cầu cho trước, hình hộp nào có diện tích toàn phần lớn nhất.

Lời giải:

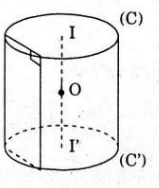
a) * Nếu H là hình lăng trụ có mặt cầu ngoại tiếp thì các mặt bên là những hình bình hành có đường tròn ngoại tiếp nên phải là hình chữ nhật. (các mặt bên là các tứ giác nội tiếp nên là hình chữ nhật).

Ngoài ra H có mặt cầu ngoại tiếp nên mặt đáy phải là đa giác có đường tròn ngoại tiếp.

* Ngược lại cho H là lăng trụ đứng có các đường tròn C và C’ ngoại tiếp các đa giác (hình vẽ).

Gọi I, I’ là tâm của C và C’ thì II’ là trục của cả hai đường tròn, gọi O là trung điểm của II’ thì điểm O cách đều tất cả các đỉnh của hình lăng trụ đã cho.

Vậy hình lăng trụ ấy có mặt cầu ngoại tiếp.

b) Nếu hình hộp H nội tiếp mặt cầu S(O, R) thì các mặt của H phải là những hình chữ nhật, vậy H là hình chữ nhật mà O là các giao điểm các đường chéo, và độ dài đường chéo d = 2R.

Gọi a, b, c là các kích thước của hình hộp chữ nhật đó thì a²+b²+c²=d²=4R². Gọi S là diện tích toàn phần của hình hộp thì ta có:

S = 2ab +2bc + 2ac ≤2(a²+b²+c² )=8R².

(chú ý hình hộp có 6 mặt là hình chữ nhật, hai mặt đối diện có diện tích bằng nhau)

Vậy S đạt giá trị lớn nhất bằng 8R² khi a = b = c = 2R/√3, tức là H là hình lập phương.