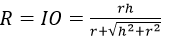Một mặt cầu gọi là nội tiếp hình nón nếu nó tiếp xúc với mặt đáy của hình nón và tiếp xúc với mọi đường sinh

Bài 4: Mặt nón, Hình nón và Khối nón

Haylamdo biên soạn và sưu tầm lời giải Bài 20 trang 60 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 20 (trang 60 sgk Hình Học 12 nâng cao): Một mặt cầu gọi là nội tiếp hình nón nếu nó tiếp xúc với mặt đáy của hình nón và tiếp xúc với mọi đường sinh của hình nón. Khi đó hình nón được gọi là ngoại tiếp mặt cầu.

a) Chứng minh rằng mọi hình nón đều có mặt cầu nội tiếp duy nhất.

b) Một hình nón có chiều cao h và bán kính bằng r. Hãy tính bán kính mặt cầu nội tiếp.

Lời giải:

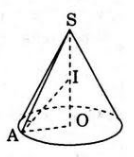
a) Giả sử hình nón đỉnh S và có đáy là đường tròn C(O, R) (hình vẽ). Lấy điểm A nào đó trên đường tròn và gọi I là điểm nằm trên SO sao cho AI là tia phân giác của góc SAO. Khi đó, khoảng cách từ I tới các đường sinh của hình nón bằng nhau và bằng IO là khoảng cách từ I tới mặt phẳng đáy. Suy ra mặt cầu tâm I bán kính r = IO chính là mặt cầu nội tiếp hình nón. Do I xác định duy nhất nên mặt cầu nội tiếp hình nón tồn tại duy nhất.

b)Ta có:

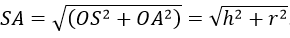
Theo tính chất đường phân giác ta có:

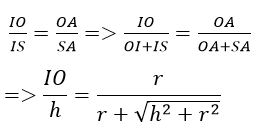
Vậy bán kính mặt cầu nội tiếp là: