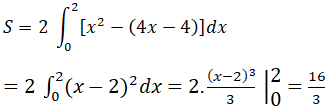Tính diện tích hình phẳng giới hạn bởi: Đồ thị hai hàm số y = x, y = 1 và y=x^2/4

Luyện tập (trang 174-175)

Haylamdo biên soạn và sưu tầm lời giải Bài 34 trang 174 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 34 (trang 174 sgk Giải Tích 12 nâng cao): Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hai hàm số y = x, y = 1 và y=x²/4 trong miền x ≥ 0;y ≤ 1

b) Đồ thị hai hàm số y=x⁴-4x²+4;y=x², trục tung và đường thẳng x = 1

c) Đồ thị các hàm số y=x²,y=4x-4 và y=-4x-4

Lời giải:

a) Cách 1.

Hoành độ giao điểm của đường thẳng y = x và y = 1 là x = 1

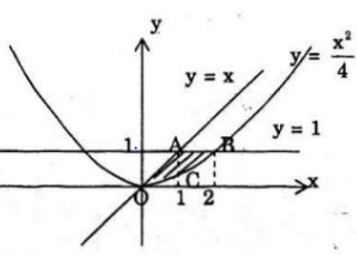
Hoành độ giao điểm của đường thẳng y= 1 và đường cong y=x²/4 trong miền x ≥ 0 là x=2.

Diện tích hình phẳng cần tìm chính là tổng diện tích tam giác cong OAC và tam giác cong ACB.

Diện tích tam giác cong OAC là:

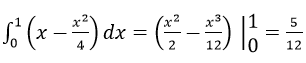
Diện tích tam giác cong ACB là:

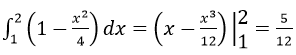
Vật diện tích hình phẳng cần tìm là:

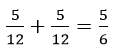
Cách 2. Gọi hình phẳng đã cho là hình phẳng giới hạn bởi đường cong có phương trình x=2 √y,dường thẳng x = y và y = 0 và đường thẳng y = 1. Diện tích cần tìm là:

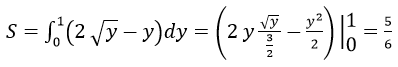
b) Diện tích hình phẳng cần tìm là:

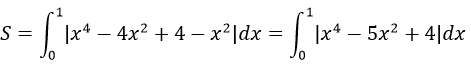
Vì x⁴-5x²+4=(x²-1)(x²-4)>-0 ∀x ∈[0;1]

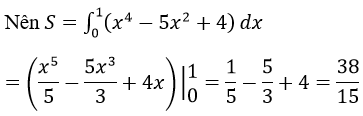
c) Ta thấy đường thẳng y=-4x-4 và đường thẳng y=4x-4 lần lượt là hai tiếp tuyến của đồ thị hàm số y=x² tại các tiếp điểm có hoành độ x = -2 và x = 2

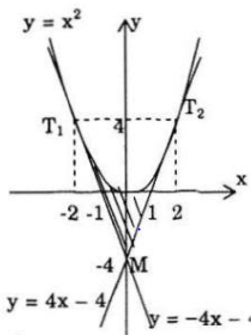
Do tính đối xứng qua Oy của parabol y=x² nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cong OMT₂ và bằng: