Tìm các tiệm cận của đồ thị hàm số sau: y = x - 2 / 3x + 2

Bài 5: Đường tiệm cận của đồ thị hàm số

Haylamdo biên soạn và sưu tầm lời giải Bài 34 trang 35 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 34 (trang 35 sgk Giải Tích 12 nâng cao): Tìm các tiệm cận của đồ thị hàm số sau:

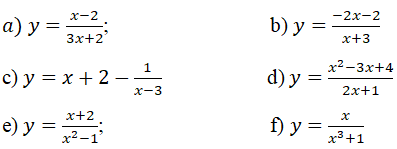
Lời giải:

a) TXĐ: D = R \ {-2/3}

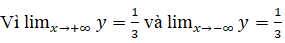
nên đường thẳng y=1/3 là tiệm cận ngang của đồ thị (khi x → +∞ và khi x → -∞)

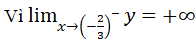
nên đường thẳng x=-2/3 là tiệm cận đứng của đồ thị x → (-2/3)^-

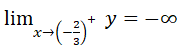
nên đường thẳng x=-2/3 là tiệm cận của đồ thị (khi x → (-2/3)⁺)

b) TXĐ: D = R \ {-3}

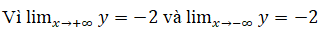
nên đường thẳng y=-2 là tiệm cận ngang của đồ thị (khi x → +∞ và khi x → -∞).

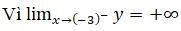
nên đường thẳng x=-3 là tiệm cận đứng của đồ thị x → (-3)^-

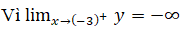
nên đường thẳng x=-3 là tiệm cận của đồ thị (khi x → (-3)⁺)

c) TXĐ: D = R\ {3}

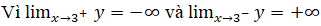
nên đường thẳng x=3 là tiệm cận đứng của đồ thị (khi x → 3^- và khi x → 3⁺ ).

Đường thẳng y=x+2 làm tiện cận xiên của đồ thị (khi x → -∞) và khi x → +∞)

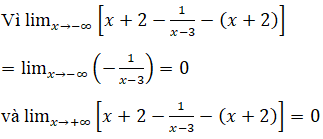
d) Cách 1. Hướng dẫn:

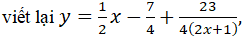
TXĐ: R \{-1/2}

Làm tương tự câu c) để có y=x/2 -7/4 là tiệm cận xiên, x=-1/2 là tiệm cận đứng.

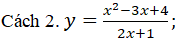
TXĐ: R \ {-1/2 }

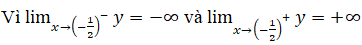
nên đường thẳng x=-1/2 là tiệm cận đứng của đồ thị (khi x → (-1/2)^- và khi x → (-1/2)⁺).

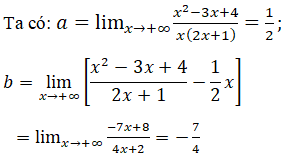
nên đường thẳng y=1/2 x-7/4 là tiệm cận xiên của đồ thị (khi x → -∞)

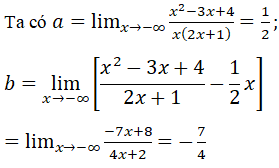
nên đường thẳng y=1/2 x-7/4 là tiệm cận xiên của đồ thị (khi x → +∞)

e) Hàm số xác định trên R \ {± 1}

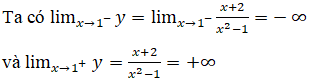
nên đường thẳng x=1 là tiệm cận đứng của đồ thị (khi x → 1^- và khi x → 1⁺).

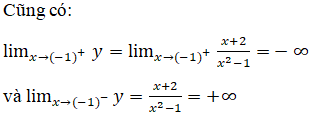
nên đường thẳng x=-1 là tiệm cận đứng của đồ thị (khi x → (-1)^- và khi x → (-1)⁺).

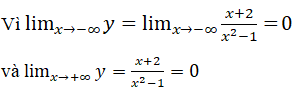
nên đường thẳng y=0 là tiệm cận ngang của đồ thị (khi x → -∞ và khi x → +∞).

Kết luận: Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x=±1 và một tiệm cận ngang là đường thẳng y = 0’

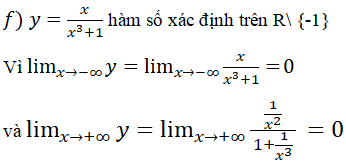
nên đường thẳng y=0 là tiệm cận ngang của đồ thị (khi x → -∞ và khi x → +∞).

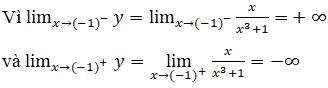
nên đường thẳng x=-1 là tiệm cận đứng của đồ thị (khi x → (-1)^- và khi x → (-1)⁺).

Kết luận: đồ thị có tiệm cận ngang là đường thẳng y =0 và tiệm cận đứng là đường thẳng x = -1