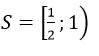Giải các bất phương trình: trang 130 sgk Giải Tích 12 nâng cao

Bài 9: Bất phương trình mũ và lôgarit

Haylamdo biên soạn và sưu tầm lời giải Bài 83 trang 130 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 83 (trang 130 sgk Giải Tích 12 nâng cao): Giải các bất phương trình:

a) log_0,1(x²+x-2)>log_0,1(x+3)    b) log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

Lời giải:

a) Bất phương trình đã cho tương đương:

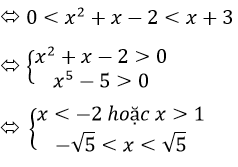
Vậy tập nghiệm của bất Phương trình là S=(-√5; -2)và (1;√5)

b) log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

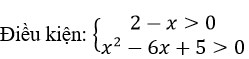
Ta có: log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

<=> log_1/3(x²-6x+5)≥log_1/3(2-x)²

<=> x²-6x+5≤(2-x)² <=> 2x-1≥0

Bất phương trình tương dương với:

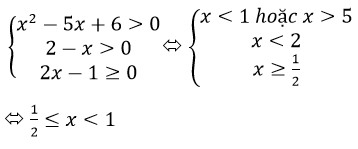
Vậy tập nghiệm của bất phương trình là: