Hàm số f có đạo hàm f’(x) = x^2 (x+1)^2(2x-1). Số điểm cực trị của hàm số là
Bài tập trắc nghiệm khách quan Chương 1
Haylamdo biên soạn và sưu tầm lời giải Bài 87 trang 65 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 87 (trang 65 sgk Giải Tích 12 nâng cao):Hàm số f có đạo hàm f’(x) = x2 (x+1)2(2x-1). Số điểm cực trị của hàm số là:
A. 1 B. 2 C. 1 D. 3
Lời giải:
Ta có:
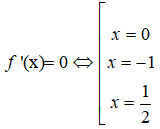
Qua điểm x = 0; x= -1 thì f’(x) không đổi dấu nên hai điểm này không là cực trị của hàm số.
Qua điểm x = 1/2 thì f’(x) đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại x = 1/2
Chọn A.

