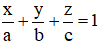Viết phương trình mặt phẳng: Đi qua điểm M 1; -2; 4
Toán lớp 12 Bài 2 : Phương trình mặt phẳng
Bài 1 (trang 80 SGK Hình học 12): Viết phương trình mặt phẳng:
a) Đi qua điểm M(1; -2; 4) và nhận n→ = (2 ; 3 ; 5) làm vec tơ pháp tuyến
b) Đi qua A(0; -1; 2) và song song với giá của mỗi vec tơ u→ = (3; 2; 1) và v→ = (-3; 0; 1).
c) Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Lời giải:
a) Mặt phẳng đi qua điểm M(1; -2; 4) và nhận n→ = (2; 3; 5) làm vectơ pháp tuyến là:
2(x – 1) + 3(y + 2) + 5(z – 4) = 0
⇔ 2x + 3y + 5z – 16 = 0.
b) Mặt phẳng nhận u→ và v→ là vec tơ chỉ phương
⇒ nhận 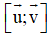
Mặt phẳng đi qua A(0 ; -1 ; 2) nên có phương trình :
2(x – 0) – 6(y + 1) + 6(z – 2) = 0
⇔ 2x – 6y + 6z – 18 = 0
⇔ x – 3y + 3z – 9 = 0.
c) Cách 1:
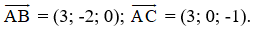
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 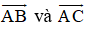
⇒ Nhận 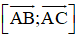
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
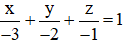
⇔ 2x + 3y + 6z + 6 = 0.
Kiến thức áp dụng
+ Phương trình mặt phẳng đi qua M(x0 ; y0 ; z0) và nhận n→ = (a ; b ; c) là vec tơ pháp tuyến :
a(x – x0) + b(y – y0) + c(z – z0) = 0.
+ Tích có hướng của u→ = (a1; a2; a3) và v→ = (b1; b2; b3) là:
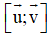
Tích có hướng 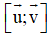
+ Mặt phẳng cắt các trục Ox; Oy; Oz lần lượt tại các điểm A(a; 0; 0); B(0; b; 0); C(0; 0; c) có dạng: