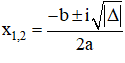Cho a, b, c ∈R,a ≠ 0,z1 , z2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình
Toán lớp 12 Bài 4 : Phương trình bậc hai với hệ số thực
Bài 4 (trang 140 SGK Giải tích 12): Cho a, b, c ∈R,a ≠ 0,z1 , z2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình ax2+bx+c=0. Hãy tính z1+z2 và z1.z2 theo hệ số a, b, c.
Lời giải:
Cách 1 :
Phương trình az2 + bz + c = 0 có Δ = b2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức 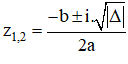
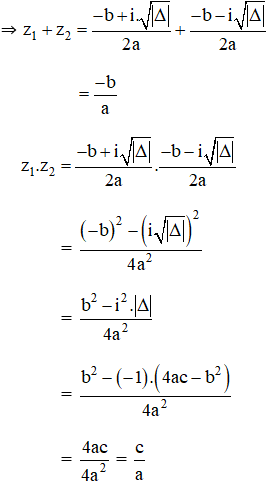
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
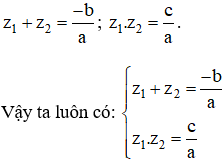
Cách 2 :
Vì z1; z2 là hai nghiệm của phương trình az2 + bz + c = 0 nên ta có:
a.z12 + bz1 + c = 0 (1)
az22 + bz2 + c = 0 (2).
+ Trừ hai vế tương ứng của (1) cho (2) ta được:
a.(z12 – z22) + b(z1 – z2) = 0
⇔ a.(z1 – z2)(z1 + z2) + b.(z1 – z2) = 0
⇔ a.(z1 + z2) + b = 0 (Vì z1 z2 nên z1 – z2 0).
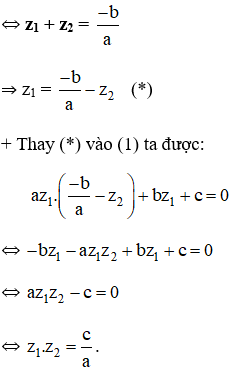
Kiến thức áp dụng
Phương trình bậc hai ax2 + bx + c = 0
có Δ = b2 - 4ac
+ Nếu Δ > 0, phương trình có hai nghiệm thực phân biệt: 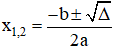
+ Nếu Δ = 0, phương trình có nghiệm kép 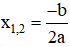
+ Nếu Δ < 0, phương trình có hai nghiệm ảo phân biệt